Bookkeepers are responsible for ensuring all financial records are accurate and up to date. It is therefore essential that you understand and apply standard mathematical techniques and methods of calculation to financial task you are asked to do, including the calculations of:
- Goods and services tax (GST)
- Simple interest
- Compound interest
- Basic loan calculations
When asked to perform a calculation, you need to have a clear understanding of the objectives for performing the calculation and the steps involved to achieve the objectives
Defining Objectives
Before you can determine the required outcome of a calculation, you need to understand the objective for performing the calculation. Ambiguity around what you are calculating may result in incorrect data or calculation methods being used.
For example, you may be asked to calculate how much GST can be claimed for professional development training provided to staff of ABC Company.
The objective in this example is to calculate the input tax credit amount ABC can claim on their Business Activity Statement for staff professional development.
Step 1: Data Collection
Once you understand the objective of the calculation, you need to collate and clarify the data required to do the calculation.
Using the example above, data you will need to collate and clarify may include:
- the cost of the training
- was GST charged by the organisation providing the training
- is the total invoiced amount GST inclusive or GST exclusive
- was any discount taken up for prompt payment
- was a deposit prepaid
Step 2: Data Analysis
After you know what data you need, you have to figure out what to do with it. This is where you attempt to take the information you collect in step one and apply it to the defined objectives. Spreadsheets and financial calculators can be used to assist you with this step.
Using the example above, we can analyse the information we have collected using a GST calculator.
The invoice received by ABC was for $1,320.00 GST inclusive. Using the GST calculator, we can calculate the amount of the GST input credit as $120.00.
GST calculator
Select the GST calculation you want to perform and enter the amount in the orange box.
| Calculate the GST on a GST exclusive amount (i.e. GST of 10%) | ||
|---|---|---|
| Enter the total amount excluding GST | $1.200.00 | |
| GST | $120.00 | |
| Total amount including GST | $1,320.00 | |
| Calculate GST on a GST inclusive amount | ||
| Total amount excluding GST | $0.00 | |
| GST | $0.00 | |
| Enter total amount including GST |
|
|
ABC received another invoice this time from a first aid training provider. The invoice was accredited CPR training and included signage for the office.
The details of the invoice were:
-CPR Training $1,000.00 GST Free
Signage $275.00 GST Inclusive
Using the GST Calculator, we can calculate the amount of the GST input credit as $25.00.
| Calculate GST for a mixed supply (invoice with both GST inclusive and GST exclusive items) | |
|---|---|
| Total amount of GST exclusive items included on tax invoice | $1,000.00 |
| Enter total amount of GST inclusive items included on tax invoice | $275.00 |
| Enter total value of tax invoice including GST | $1275.00 |
| GST | $25.00 |
Credit is when a contractual agreement is made, in which a borrower receives something of value (money) and agrees to repay the lender, generally with interest, within a set time frame in the future. Interest can also be referred to as the borrowing capacity of an individual or company.
Interest is the fee charged by the lender to a borrower for the use of borrowed money, typically expressed as an annual percentage of the principal. The rate depends on the time value of money, the credit risk of the borrower, and the inflation rate.
A crucial part of understanding how well you are managing your business and your finances is the ability to calculate interest. Interest rates have an impact on all businesses because they not only affect the cost of borrowing money and therefore the cost of doing business., they are also a critical factor in making money grow.
Below we will look at some of the common calculations you will be required to perform when working as a bookkeeper or accountant.
Business loans
What is a business loan?
- it is money you borrow from a bank or financial institution
-Helps you start a business
-Comes with either a fixed or variable interest rate
-Can be secured or unsecured
A business loan is any type of financing that’s used to fund business expenses.
There are a variety of business loan options to choose from. These include:
- Bank loans: Bank loans are one of the most common forms of finance for small and medium-sized businesses. They can vary in the amount, loan term (the period in which you repay the loan), interest rate, interest rate type (fixed or variable), fees and security.
- Business Overdraft: A business overdraft is a facility attached to a bank account with an authorised overdraft limit. An overdraft occurs when you make a transaction for an amount greater than the balance in your account. The bank then extends credit up to a maximum overdraft limit, and you can make withdrawals up to that limit. Interest is charged on the fluctuating daily balance, but the overdraft balance does not need to be repaid within a set timeframe.
- Line of credit: A line of credit provides a business with access to funds by allowing it to draw on an account balance up to an approved limit. As long as the balance does not go over the limit, funds can be drawn at any time.
- Commercial bill (also known as a bill of exchange): A commercial bill is a type of loan for short-term funding needs, such as inventory. You get a fixed sum advance with a regular interest payment. The final amount is due at the end of the term.
Loan repayment terms can last anywhere from 12 months to 25 years.
The Australian small business and family Enterprise Ombudsman has produced a resource for small businesses to assist them in finding the right funding option for their business.
Check out the 'Business Funding Guide'. A guide to small business on getting the right funding for you
Basic loan calculations
The type of calculation you use will vary based on the type of loan.
Interest-only loans
With interest-only loans, you don’t pay down any of the principal in the early years—only interest. The amount that you owe on the loan does not go down with each payment. Once the interest-only period ends, you may have several options:
- Paying off the loan balance all at once
- Refinancing the mortgage loan, if refinancing is available
- Beginning to pay off the balance in monthly payments, which are higher than the interest-only payments.
To calculating payments for an interest-only loan, multiply the amount you borrow (a) by the annual interest rate (r), then divide by the number of payments per year (n). Or, multiply the amount you borrow (a) by the monthly interest rate, which is the annual interest rate (r) divided by 12:4.
\begin{equation} A\frac{r}{n} \end{equation}
A= amount borrowed
r = the annual interest rate (decimal)
n = the number of payments per year
Example
James borrows $100,000 at 6% for 15 years. Interest is to be repaid monthly.
First convert the interest rate to a decimal format.
- Amount = $100,000
- Rate = 6.0% = .06
- Number of payments per year = 12
\begin{equation} 100,000 ×\frac{.06}{12} \end{equation}
Interest = $500/month
Amortising loans
An amortised loan is one where the principal of the loan is paid down according to an amortisation schedule, typically through equal monthly instalments. A portion of each loan payment will go towards the principal of the loan, and the remainder will go towards interest charges.
Many financial institutions have loan calculators to assist you in working out monthly repayments and total repayments.
Example
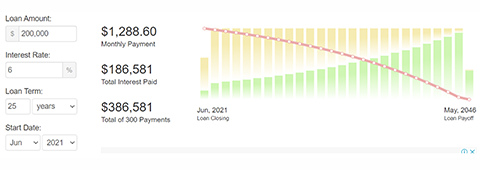
James borrows $200,000 at 6% for 25 years to be repaid monthly.
Calculate the monthly repayment using a loan calculator = $1,288.60
Calculate the total interest paid $186,581
Calculate the total amount James will pay after 25 years = $386,581
Credit card loans
When using a credit card, you're given a line of credit that acts as a reusable loan so long as you pay it off in time. If you're late on making monthly payments and begin to carry a balance, you'll likely be charged interest.
Credit card balance constantly fluctuate. Therefore, financial institutions typically use a formula to calculate the minimum monthly payment based on the total balance owing.
Example
The card issuer might require you to pay a minimum payment of $50.00 or 1.5% of the outstanding balance every month.
The business owes $15,500 on its credit card. What is the minimum monthly repayment.
Minimum Repayment = $15,500
Rate = 1.50% = .015
$15,500 x .015
Interest = $232.50
It can be difficult to understand exactly how much you'll pay when evaluating several competing loan offers. For example, one might have a lower interest rate, while another offers lower fees. Deciding which offer to choose means you'll need to calculate the total cost of the loan, including interest and fees. Calculators can help when making comparisons.
Source - Understanding Compound Interest (investopedia.com)

When an investor lends money to a borrower, the borrower must pay back the money originally borrowed, called the principal, and the fee charged for using the money, called interest. The sum of the principal and interest is called the accumulated value.
The following formula can be used to calculate simple interest:
Interest = principal x rate x term
or
I = Prt
I = interest rate
P = the principal investment amount (the initial deposit or loan amount)
r = the annual interest rate (decimal)
t = the time the money is invested or borrowed for
When you pay back a loan with simple interest, you pay the principal amount plus the total interest on that amount. This amount is called the accumulated value.
To calculate the accumulated value following formula is used:
Amount = principal + interest
or
S = P + I
S = the amount of money paid back at the end of the loan
Example
Trent Smith applied to ANZ for a 4-year loan of $8,000. The bank approved the loan at an annual interest rate of 6.5%.
What is the simple interest on the loan?
Principal = $8,000
Rate = 6.5% = .065
Time = 4 years
Prt = I
$8,000 x .065 x 4 = $2,080
Interest = $2,080
What is the accumulated value of the loan?
Principal = $8,000
Interest = $2,080
P + I = A
$8,000 + $2,080 = $10,080
The life of a loan may be referred to in days, months or years; however, the rate of interest is an annual rate. Therefore, if the duration of a loan is expressed in days or months, the time must be converted to years.
When the time (t) is given in months, the formula to convert it to years is:
\begin{equation} t=\frac{No. of months}{12} \end{equation}
Example
Marion Jones was approved for a loan of $6,500. The interest rate on the loan is 8.25%, and the term of the loan is for 9 months. What is the accumulated value of the loan?
P = $6,500
r = 8.25% = 0.0825
t = 9 months
\begin{equation} t=\frac{9}{12} \end{equation}
I = Prt
\begin{equation} $6500.00 × 0.0825 × \frac{9}{12} \end{equation}
= $402.19
P + I = A
$6500.00 + $402.19 = $6902.19
As the interest rate has changed during the period, the interest has to be calculated separately for each period. When calculating the exact number of days between two dates, the end date is subtracted from the start date. The reason being financial institutions calculate interest each day on the closing balance. So the day the deposit is taken out, or a loan commences, there will be a balance at the end of the day. On the day the deposit is withdrawn or the loan is paid off, there will be a zero balance at the end of the day.
Example
Jordan deposited $13,000 into a fund on 5 March, earning 4.75% interest per annum. On 15 August, the interest rate changed to 5.25% per annum. What was the balance of Jordan’s fund on 30 November?
Period 1: 5 March - 15 August
| Month | Number of days |
|---|---|
| March | 31-5 = 26 |
| April | 30 |
| May | 31 |
| June | 30 |
| July | 31 |
| August | 15 |
| TOTAL | 163 |
Period 2: 16 August - 30 November
| Month | Number of days |
|---|---|
| August | 31-15 = 16 |
| September | 30 |
| October | 31 |
| November | 30 |
| TOTAL | 107 |
A = original deposit + interest for 163 days + interest for 107 days
\begin{equation} = $13,000 + ($13,000 × .0475 ×\frac{163}{365}) + ($13,000 × .0525 ×\frac{107}{365}) \end{equation}
= $13,000 + $275.76 + $200.08
= $13,475.84
Declining balance
Financial obligations are sometimes liquidated by a series of partial payments throughout the term of the obligation. Partial payments on debts over the term of the obligation require the recomputation of the balance due on the final date.
Declining balance method requires the interest on the unpaid balance to be computed each time a partial payment is made. If the payment is more than the interest due amount, the difference is used to reduce the debt.
Example
On 4 January, Molly borrows $5000 at a simple interest rate of 8.75% per annum. She pays:
- $1000 on 21 March
- $850 on 15 April
- $1250 on 31 July
What is the balance due on 25 August using the declining balance method?
| Dates | Number of days |
|---|---|
| January 4 - 21 March | 76 |
| 21 March - 15 April | 25 |
| 15 April - 31 July | 107 |
| 31 July - 25 August | 25 |
| Original debt | $5000.00 |
| Interest 76 days | $91.10 |
| Amount due 21 March | $5091.10 |
| First partial payment | $1000.00 |
| Amount due 21 March | $4091.10 |
| Interest 25 days | $24.52 |
| Amount due 15 April | $4115.62 |
| Second partial payment | $850.00 |
| Amount due 15 April | $3265.62 |
| Interest 107 days | $83.77 |
| Amount due 31 July | $3349.39 |
| Third partial payment | $1250.00 |
| Amount due 31 July | $2099.39 |
| Interest 25 days | $12.58 |
| Amount due 25 August | $2111.97 |
How to Calculate Simple Interest in Excel
To assist you in calculating simple interest we have developed this Simple Interest Calculator. Click here to access the calculator.
Calculating simple interest
Enter the loan information in the orange box.
| Calculate simple annual interest with no compounding | |
|---|---|
| Amount (principle) | 1000 |
| Interest rate | 5.00% |
| Terms (years) | 10 |
| Interest | 500 |
Compounding interest is interest that accrues on the principal and the accumulated interest of a loan or debt. The principal and total interest are referred to as the compound amount. The difference between the compound amount and the principal amount is called the compound interest.
What does the different frequency or occurrence of the compounding make to your savings calculation?
The line graph below demonstrates the compounding effect of varying rates on an initial investment of $1000 with a 20% annual interest rate.
Interest can be calculated at the start or the end of the compounding period (month or year) when it comes to savings accounts.
The formula for compound interest is [Math Processing Error]
A = the future value of the investment/loan, including interest
P = the principal investment amount (the initial deposit or loan amount)
r = the annual interest rate (written in a decimal format)
n = the number of times that interest is compounded per unit of t
t = the time the money is invested or borrowed for
Sam deposits $5,000 into a savings account at an annual interest rate of 5%, compounded monthly. What is the value of Sams investment after 10 years?
- P = 5000.
- r = 5%
- n = 12
- t = 10
First, convert r as a percent to r as a decimal.
r = r/100
r = 5/100
r = 0.05 rate per year.
\begin{equation} A = $5,000 (1 +\frac{0.05}{12}) ^{12 × 10} \end{equation}
Then solve the equation for A.
A = P(1 + r/n)nt
A = 5,000.00(1 + 0.05/12)(12)(10)
A = 5,000.00(1 + 0.004166667)(120)
A = $8,235.05
The total amount accrued, principal plus interest, with compound interest on a principal of $5,000.00 at a rate of 5% per year compounded 12 times per year over 10 years is $8,235.05.
Jane deposits $7000 into an account that earns 3% interest.
Calculate the amount in the account after 15 years if the interest compounds monthly.
\begin{equation} A = $7,000 (1 +\frac{0.03}{12}) ^{12 × 15} \end{equation}A = $7,000 (1.0025)180
A = $7,000 (1.56743172466)
A = $10,972.02
Calculate the total amount of interest earned after 12 years.
A-P=I
$10,972.02 - $7,000 = $3972.02
Many financial institutions have compounding interest calculators on their websites which allow customers to calculate compound interest on either a daily, monthly, quarterly, half-yearly or annual basis.
Compound Interest
To calculate compound interest in Excel, you can use the FV function.
Using the same example above.
Sam deposits $5,000 into a savings account at an annual interest rate of 5%, compounded monthly. What is the value of Sam’s investment after 10 years?
Compound interest calculation
| Present value | $5,000.00 |
| Interest rate | 5.00% |
| Terms (years) | 10 |
| Compounding periods per year | 12 |
| Future value | $8,235.05 |
Generic formula = FV(rate,nper,pmt,pv)
=FV(C8/C10,C9*C10,0,-C7)
The FV function can calculate compound interest and return the future value of an investment. To configure the function, we need:
- a rate
- the number of periods
- the periodic payment
- the present value.
To get the rate (which is the period rate) we use the annual rate / periods, or C8/C10.
To get the number of periods (nper) we use term * periods, or C9 * C10.
There is no periodic payment, so we use zero.
The present value (pv) is input as a negative value, since the $1000 "leaves your wallet" and goes to the bank during the term.
The solution is calculated this way:
=FV(C8/C10,C9*C10,0,-C7)
=FV(0.05/12,10*12,0,-5000)
=FV(0.00417,120,0,-5000)
=FV $8235.05

Goods and services tax
Goods and services tax (GST) is a broad-based tax of 10% on most goods, services, and other items sold or consumed in Australia.
Organisations must register for GST if:
- their business income is $75,000 or more
- they are a non-profit organisation and have a business income of $150,000 or more
- they provide taxi or limousine travel (including ride-sourcing services like Uber, GoCatch, Didi or OLA)
- they want to claim fuel tax credits for their business
Special rules may apply to non-residents. Otherwise, registration for GST is optional.
Businesses registered for GST must add GST to the price of the goods or services they sell and issue a tax invoice to their customers.
When a business buys something, they are usually charged GST. However, if the business is registered for GST, it can claim the GST back. They do this by claiming a GST tax credit when lodging their business activity statement (BAS).
GST is described as an end user tax. The diagram below explains how GST is charged and claimed back by businesses registered for GST. It is ultimately the consumer (end user) who is responsible for paying the GST.
Source How to Calculate GST | Your Guide to GST and BAS | Xero AU
Requirements of tax invoice
Tax invoices are different to regular invoices. They include the GST amount for each item (or state that the total price includes GST) and some extra details.
Tax invoices for sales under $1,000
Tax invoices for taxable sales of less than $1,000 must include enough information to clearly determine the following seven details:
- that the document is intended to be a tax invoice
- the seller's identity
- the seller's Australian business number (ABN)
- the date the invoice was issued
- brief description of the items sold, including the quantity (if applicable) and the price
- the GST amount (if any) payable – this can be shown separately or, if the GST amount is exactly one-eleventh of the total price, such as a statement which says 'Total price includes GST.'
- the extent to which each sale on the invoice is a taxable sale
Tax invoices for sales of $1,000 or more
Tax invoices for sales of $1,000 or more need to show the buyer's identity or ABN.
If your tax invoices meet the requirements for sales of $1,000 or more, you can also use them for sales of lesser amounts. The example above shows:
- GST included in each line item
- the sale is clearly identified as being fully taxable by the words 'Total price includes GST.'
- the buyer's identity for sales over $1,000.
Source Tax invoices | Australian Taxation Office (ato.gov.au)
How to calculate GST
When a business sells goods or services, it adds 10% to the cost of the item or service to arrive at a price charged to the customer.
To calculate the amount of GST to be included on an invoice, divide the value of the sale by 10.
$185.00 ÷ 10 = $18.50
GST amount = $18.50
To calculate the total price to charge a customer, you add the GST amount to the sale amount.
Cost of Item + GST = Total price
$185.00 + $18.50 = $203.50
To calculate the amount of GST included in a price, you divide the price by 11.
Invoiced amount ÷ 11 = GST
$203.50 ÷ 11 = $18.50
Example
Fast Fencing is registered for GST and bought 500mts of wire at $5.00 per meter. Calculate:
- The cost of the wire.
- The Amount of GST Fast fencing can claim as an Input tax credit.
- Calculate the total cost Fast Fencing will be invoiced
First, calculate the cost of the wire
500 x $5.00 = $2,500.00
Second, calculate the GST
$2,500 ÷ 10 = $250.00
Finally, add the GST to the cost
$2,500.00 + $250 = $2,750.00
For more information on GST, refer to Xero small business guide – Your quick guide to GST and BAS in Australia.
GST Calculator
To assist you in calculating GST we have developed this GST calculator. Click here to access the calculator.
| Calculate the GST on a GST exclusive amount (i.e. GST of 10%) | |
|---|---|
| Enter the total amount excluding GST | $100.00 |
| GST | $10.00 |
| Total amount including GST | $110.00 |
| Calculate GST on a GST inclusive amount | |
| Total amount excluding GST | $100.00 |
| GST | $10.00 |
| Enter total amount including GST | $110.00 |
| Calculate the GST for mixed supply (invoice with both GST inclusive and GST exclusive items) | |
| Total amount of GST exclusive items included on the tax invoice | $90.00 |
| Enter total amount of GST inclusive items included on the tax invoice | $110.00 |
| Enter total value of the tax invoice including GST | $200.00 |
| GST | $10.00 |

