Welcome to the second module of your Level 3 Certificate in Electrical Pre-Trade.
You will start out with some algebra. The electrical trade involves a lot of calculation, and it is important you are comfortable manipulating the various formulae. There will be lots of opportunity to practice your skills in the following modules and in the workshop. Correct calculations are critical!
Next you will have the opportunity to learn about and practice circuitry. You should become familiar with conductors and insulators, as well as the various measurements in a circuit – voltage, current, resistance and power. Learning the theory of correctly connecting components in a circuit will give you the confidence to build circuits in the workshop.
Learning about electromagnetic induction provides the foundation for understanding motors, generators and transformers.
The final part of this module focuses on AC generation and involves some more mathematical concepts – namely the sinusoidal waveform. It also touches on vector quantities with the introduction of impedance.
| Credits | 38 |
| Learning Hours | 380 |
| Learning Outcome | LO 2.1 Apply mathematical principles to basic electrical tasks. LO 2.2 Apply knowledge of conductors, insulators, semiconductors, resistors and resistivity to basic electrical tasks. LO 2.3 Apply knowledge of Ohm’s law when working with basic electrical circuits. LO 2.4 Apply knowledge of Electromotive force (e.m.f) production to basic electrical tasks. LO 2.5 Apply knowledge of electromagnetic theory to basic electrical tasks. LO 2.6 Apply knowledge of DC circuits and relevant calculations on power, cost and energy to basic electrical tasks. LO 2.7 Apply knowledge of electronics, protection from interference and special power supplies to basic electrical tasks |
| Assessment | ELE02A ELE02B ELE02C ELE02D ELE02E |
You are free to plan your studies in the way that works best for you, but we know that guidance on how to do this is also helpful. We suggest following way to navigate through the learning content over the next few weeks:
| Week 1 | Topic 1 Electrical Calculations |
| Week 2 | Topics 2 Conductors, Insulators, Semiconductors and Resistors |
| Week 3 | Topic 2 Conductors, Insulators, Semiconductors and Resistors |
| Week 4 | Topic 3 Ohm’s Law |
| Week 5 | Topic 4 Electromagnetic Theory |
| Week 6 | Topic 4 Electromagnetic Theory |
| Week 7 | Topic 5 DC (Direct Current) Circuits |
| Week 8 | Topic 5 DC (Direct Current) Circuits |
| Week 9 | Topic 5 DC (Direct Current) Circuits |
| Week 10 | Topic 6 Electronic Components |
| Week 11 | Topic 7 Review all SDL tasks and glossary to ensure all content has been covered. |

What we're covering:
- Algebra overview
- Algebra practice
- V=IR
So far, we’ve focused on legislations and how to stay safe in the electrical industry. Now it’s time to look at electrical formulae and solving mathematical equations.
This video gives an overview of Algebra and introduces the concepts of unknown values and variables. (Even if you feel pretty confident about this section, it is still valuable to watch these videos.)
This video shows you how to solve simple 1- step Algebra equations involving only addition or subtraction.
Activity
Now solve these equations using the method shown in the video. Write your answers down on a piece of paper. Check with your tutor when you are done (email or chat via the LMS).
- 26 = 8 + v
- 3 + p = 8
- x – 7 = 13
- m – 9 = −13
- n + 16 = 9
This third video shows you how to solve simple 1- step Algebra equations involving multiplication and division.
Activity
Once again, solve these equations using the method shown in the video.
- 3x = 48
- 17 = a/2
- r/8 = 4
- 0.55 = 1.1p
For the following questions, use the electrical formula V = IR to solve for the missing variable.
- A wire carrying a current (I) of 4 Amperes has a resistance (R) of 5 ohm. Calculate the potential difference (voltage) across its ends.
- What voltage will produce a 0.35 Ampere current (I) through a 750 ohm resistor (R)?
- A hair dryer draws a current (I) of 7.5 Amperes when it is plugged into a 240 Volt outlet. What is the resistance of the hair dryer?
- The heating element in an electric heater has a resistance of 12.5 ohm. What will be the current through the heating element when it is connected to a 240 Volt source?
- A water heater with a rated wattage (Power, P) of 1200 Watts is connected to a 120 Volt power supply.
- What is the current? (Use P = VI)
- What is the resistance of the heater? (Use R = V/I)
- Can you solve this riddle? (Answers will be provided at the end of this week of learning)
What we're covering:
- The rules of transposing
- Practicing transposing
Sometimes, in order to solve an equation, it is necessary to transpose or rearrange the formula first. Consider the formula for calculating velocity, v.
v = u + at
Suppose you already knew the values for v, u and a and you wanted to calculate t. This would require you to do some rearranging to find the expression for t.
t = (v - u)/a
So how do we rearrange or transpose formulae? Watch these two videos (several times if necessary) to learn the steps.
The important rule to remember is that whatever you do to one side, you must also do to the whole of the other side. For example, you may:
- Add the same quantity to both sides.
- Subtract the same quantity from both sides.
- Multiply or divide both sides by the same quantity.
- Perform operations on both sides such as ‘square both sides’, ‘square root both sides’, etc.
Activity
You will find lots of examples of transposing formulae at this site. This worksheet is an example. Download it and practice until you feel confident transposing.
Activity
Try out your skills with these two puzzles. Write your answers on a piece of paper. Ask your classmates in the forum if you need help. You will know you are on the right track if you all get the same answers. (Answers provided at the end of this week of learning)
 |
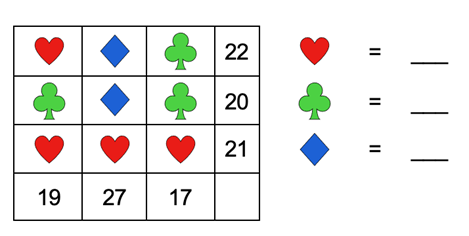 |
Activity
Dominoes
Drag and drop the dominoes to correctly match the scientific notation to the ordinary decimal form.
Activity
Magic Square
Drag and drop the squares to correctly match the scientific notation on one edge to the ordinary decimal form on the edge of another square. (Your final square should be 4 x 4.)
What we're covering:
- getting to know your scientific calculator.
- basics
- corrections
- exponents and roots
- scientific notation
- factions and decimals
It is very important you know how to use a scientific calculator. Look at the following electrical engineering formulas and equations for the basic quantities, i.e., current, voltage, power, resistance and impedance in both DC and AC circuits (single phase and three phase).
| Quantity | DC | Single Phase AC | Three Phase AC |
|---|---|---|---|
| Current (I) amp |
|
|
I = P / ∛ x V x Cos8 |
| Voltage (V) volts |
|
|
|
| Power (P) watts |
|
|
|
| Resistance (R) Ω |
|
|
|
You will need to perform calculations that involve brackets, fractions, exponents and roots, and even some trigonometry (in later studies.)
Getting to know your calculator
The first step in using your calculator effectively is to make sure that you are familiar with the layout of the keys on the keypad, and that you can understand the information on the display.
1. Basic Calculations
Basic calculations are entered into the calculator in exactly the same order as they are written on paper. The calculator displays the calculation that you enter.
When you press the “equals” button, the answer is displayed on the screen.
Use your calculator to work out the answers to the following calculations and check you get the correct answer.
- 3298 + 76 x 258 =
- 4644 / 86 – 19 =
- 65 x (3106 – 999) =
- (98,352 + 321) x (63,051 – 49,872) =
What happens if we don’t insert brackets in the last two questions? Try it…
Recall the BEDMAS rules which states that:
- any expression within Brackets should be calculated first,
- then any Exponents (also called powers or indices),
- followed by Divisions and Multiplications,
- and finally, Additions and Subtractions.
Note: BEDMAS is sometimes referred to as PEMDAS where the P means parenthesis (another word for brackets)
Example: The call out fees for 3 jobs were $50, $62 and $73. Which of these sequences is better for finding the average call out fee for these 3 jobs?

2. Using your calculator for negative numbers
There are two different mathematical uses for the minus sign (-):
- as the symbol for subtraction, such as 7 – 3
- to indicate a negative number, such as -2
Most calculators have two different minus sign buttons corresponding to these two different functions:
- when you are subtracting, choose -
- but when you want to enter a negative number choose either or +/- or (-).
3. Making corrections
If you make a mistake when entering a key sequence into the calculator, you can correct your error without having to start all over again.
The < and > keys on the large cursor control button allow you to move the cursor (shown on the display as a vertical line, |) to the spot in the calculation where you want to make a correction.
The DEL key is useful to delete items to the left of the cursor, whereas the ‘all clear’ AC key completely deletes the calculation and clears the screen.
4. Exponents and Roots
There are several keys on the calculator that enable you to perform calculations involving exponents or powers. Small exponents such as squares or cubes often have their own buttons, X2 and X3 - can you locate these on your calculator?
e.g., for 62 you would press 6 then X2
and for 63 you would press 6 then X3
To calculate higher powers, for example 65, you need to use the general exponent key which could look like one of these:
^ or Yx or XY
To find 65, press 6 then the exponent key, and lastly the exponent - 5
Use your calculator to work out the answers to the following calculations and check you get the correct answer.
- 3452 =
- 86 =
- 93 – 39 =
Just as there are keys on your calculator for entering exponents, roots can also be entered directly.
Square roots can be calculated using the square root key, which will look like one of these:
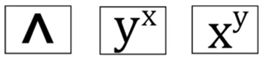
Cube roots may also have their own button:
For higher roots, like fourth or fifth roots, use the general button:
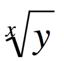
(This button can also be used for square roots and cube roots too.)
Use your calculator to work out the answers to the following calculations and check you get the correct answer. (Answers will be provided at the end of this week's learning)
5. Scientific notation on your calculator
If the answer to a calculation is > (greater than or equal to) 1010 (10,000,000,000) the calculator automatically displays the answer in scientific notation.
- e.g., Calculate 2010. Your calculator will probably display 1.024e13 or 1.024 x 1013
Very small numbers may also be displayed using scientific notation.
- Calculating 5-10 should display as 1.024e-07 or 1.024 x 10-07.
To input numbers in scientific notation, use the EE or EXP button. Your calculator should have a button for using scientific notation labelled either "EE" or "Exp". (It may be actually printed ON a button or printed ABOVE a button.)
- To input 9.1 x 104 press 9.1 “EE” 4 = 91,000 (If you don’t have the EE button, you can always use x 10 ^ i.e., 9.1 x 10 ^4 =)
Use your calculator to work out the answers to the following calculations and check you get the correct answer.
- 0.68 x (4.6 x 107) =
- (7.5 x 1012) / (3.2 x 106) =
- (4 x 10-3) + (5 x 10-4) =
6. Fractions and Decimals
When your calculator is in Math mode (recommended) the result of a calculation that is not a whole number, will be displayed as a fraction.
To switch between fraction and decimal forms press the fraction button which may look like: ![]() or
or ![]() or
or ![]()
Use your calculator to work out the answers, in both fractional and decimal forms, to the following calculations. Check you get the correct answer. (Answers will be provided at the end of this week's learning)
- 468 / 585 =
- 3654 / 252 =
- 16.125 x 3.02 =
Following is a selection of videos covering some of the essential calculator covered above. View any topics you are still not feeling confident about.
- Electronics Tutorial 3 - How to use Your Calculator
- How to Use Your Scientific Calculator. (Watch as far as 4.31 minutes to learn how to convert a number into scientific notation, how to use, fractions, percentages, roots, exponents and parentheses. This doesn’t just apply to chemistry.)
- How to use your calculator for scientific notation.
- Casio Calculator Tutorial - Overview of Essential Buttons
- How to Use a Calculator
Activity
If you are not feeling completely overloaded with numbers right now test yourself with these two exercises on using a calculator and standard form.
