Topic 6: Simultaneous Equations

Submitted by sam.hopley@up… on Thu, 08/03/2023 - 12:00
Sub Topics
Learning Aims – Simultaneous Equations

By the end of this topic, you should be able to:

  • Solve 2 × 2 system of equations
  • Solve 3 × 3 system of equations
  • Understand and describe geometric interpretations
  • Write simultaneous equations to solve problems

Introduction

Simultaneous means to occur, happen, or be done at the same time.

Simultaneous equations are a set of different equations that are all true when the variables have the same value in each equation. A set of simultaneous equations is often called a system of equations.

To solve a set of simultaneous equations, you need to find the values of the variables that satisfy all the equations simultaneously. It is not always possible to solve equations simultaneously.

Simultaneous equations are used to solve everyday problems that involve more than one variable. The following are some common situations in which you could use simultaneous equations to find the solution to the problem. Use the arrows to move between the different examples.

Overview

In this topic, you will work with linear equations. In other words, all the variables are to the power of 1.

The following are examples of linear equations:

$$\begin{aligned}2x+5y&=10\\x-8y+z&=3\end{aligned}$$

Each term in a linear equation consists of either a constant (from the previous examples, 10 and 3) or a multiple of a variable to the power of 1 . Variable terms include at least one pronumeral \((x,\;y\) or \(z)\) and the coefficient. Here, the \(x\)-coefficients are 2 and 1; the \(y\)-coefficients are 5 and −8; and the \(z\)-coefficient is 1. When the coefficient is 1, no number is written.

Variables are sometimes called unknowns since their values are not (yet) known.

The linear equation \(2x+5y=10\) has two unknown variables, \(x\) and \(y\).

The linear equation \(x-8y+z=3\) has three unknown variables, \(x\), \(y\) and \(z\).

Check your understanding

Complete the following three (3) tasks. Click the arrows to navigate between the tasks. You may attempt this activity as many times as you like.

All tasks refer to the following equation:

$$−7p+q-4r=6$$

A linear equation with two unknown variables represents a straight line in 2-dimensional space (in other words, in the plane). This is why these types of equations are called linear equations.

For example, the following linear equation can be rearranged into the familiar straight line formula.

$$\begin{aligned}2x+5y&=10\\y&=\frac{-2}{5}\times2\end{aligned}$$

Where the gradient and y-intercept can be read directly from the equation.

$$\begin{aligned}\mathsf{Gradient}&=\frac{-2}{5}\\y{\text -}\mathsf{intercept}&= 2\end{aligned}$$

When solving two linear equations with two unknown variables, your aim is to find a single value for each variable that satisfies each of the simultaneous equations.

Consider the two simultaneous linear equations with two unknown variables:

$$\begin{aligned}2x+5y&=17&&\mathsf{Equation}\;(1)\\5x-y&=29&&\mathsf{Equation}\;(2)\end{aligned}$$

When solved, the following values for each variable are obtained:

$$\begin{aligned}x=6, y=1\end{aligned}$$

These values satisfy the pair of simultaneous equations because the same values make both equations true. When graphed, the simultaneous solution is the point of intersection between the two lines. The following graph demonstrates the unique solution of these two simultaneous equations, where 'A' is the point of intersection.

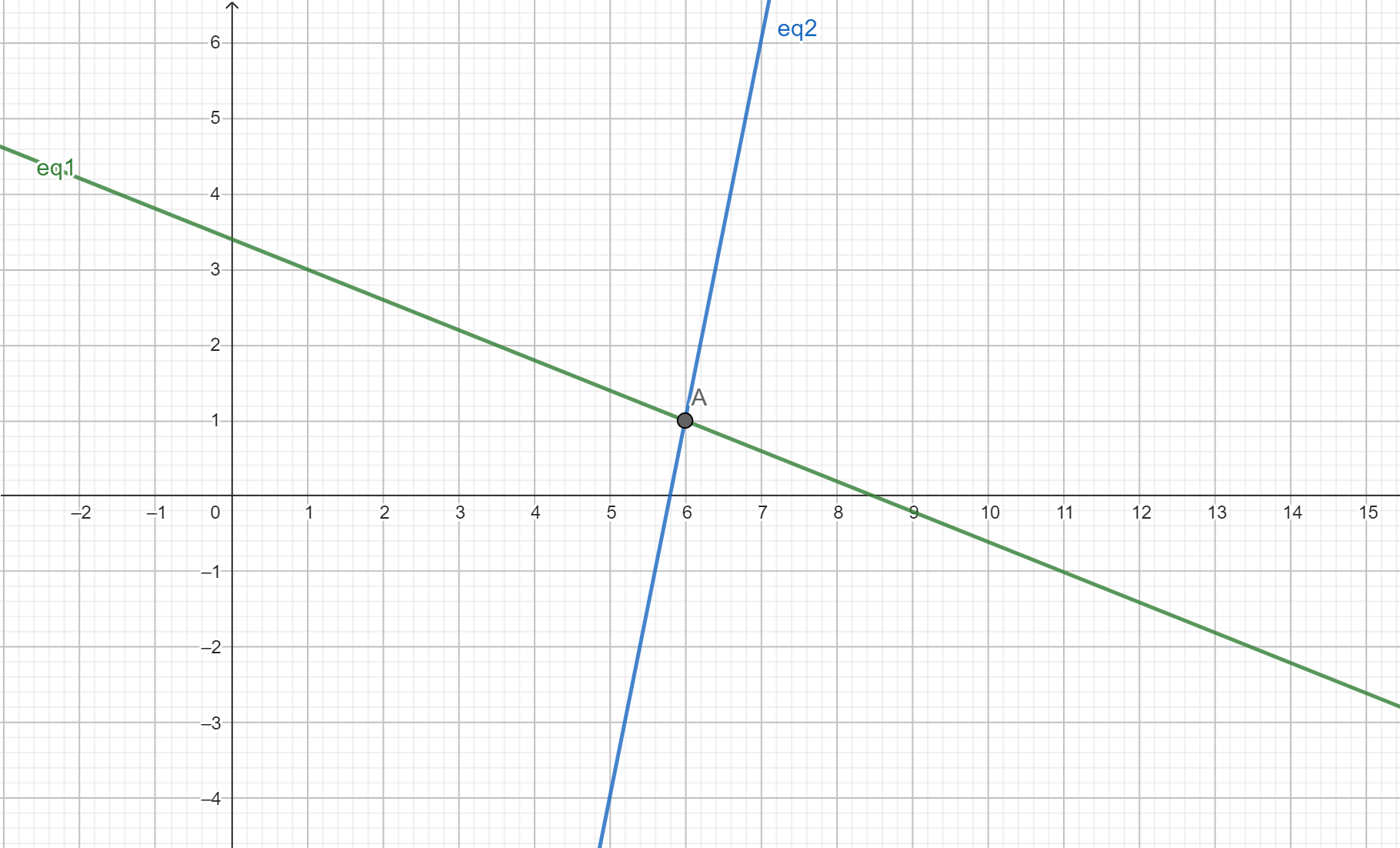
Geometric Interpretations - Two Linear Equations with Two Unknowns

There are three possible outcomes when attempting to solve two linear equations with two unknown variables simultaneously:

  1. A unique solution
  2. Multiple solutions
  3. No solution.

These three outcomes are summarised in the following table.

Outcome Unique Solution Multiple Solutions No Solution
Geometric Interpretation Non-parallel straight lines Coincident straight lines Parallel straight lines
Graphic Representation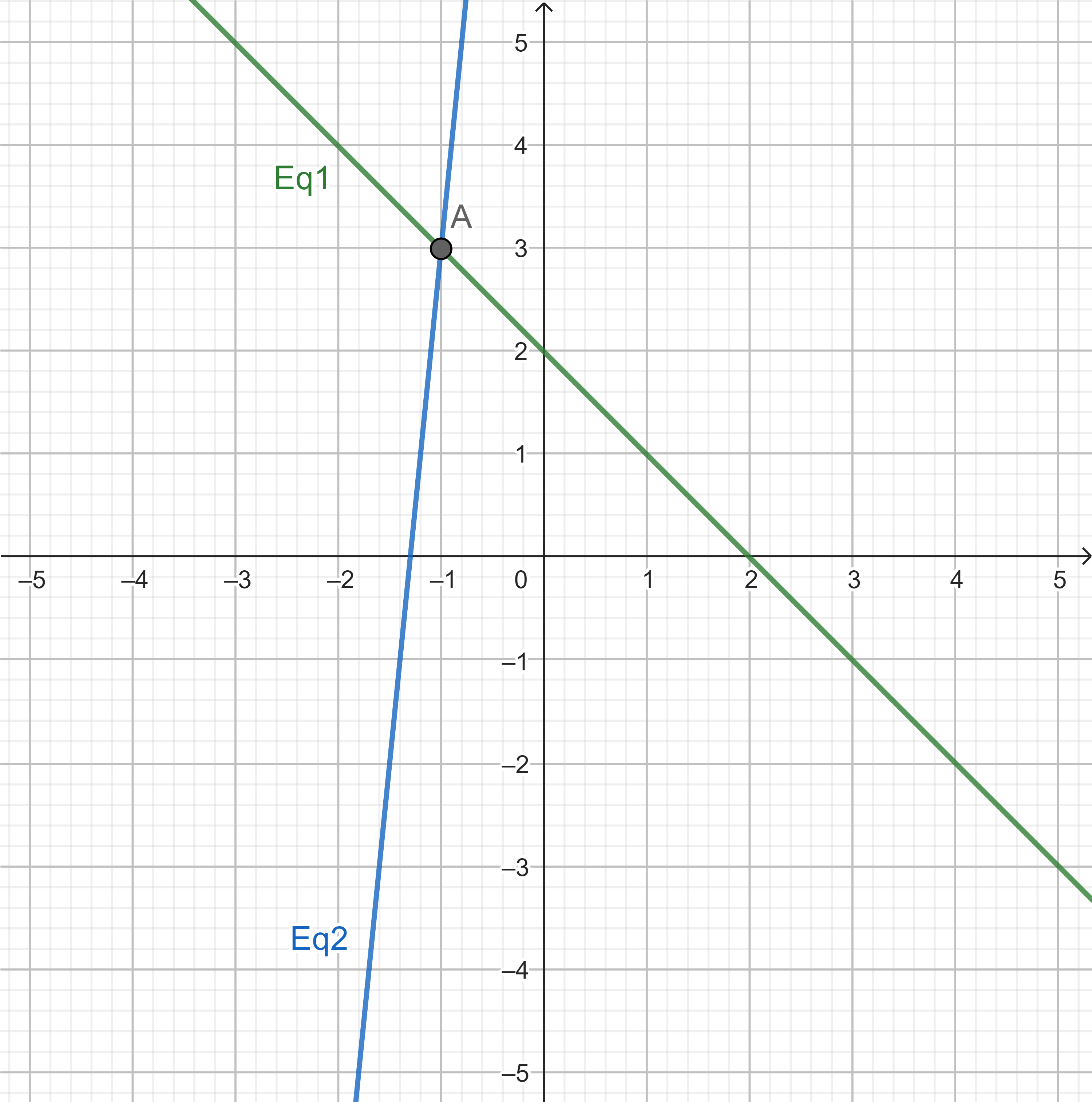
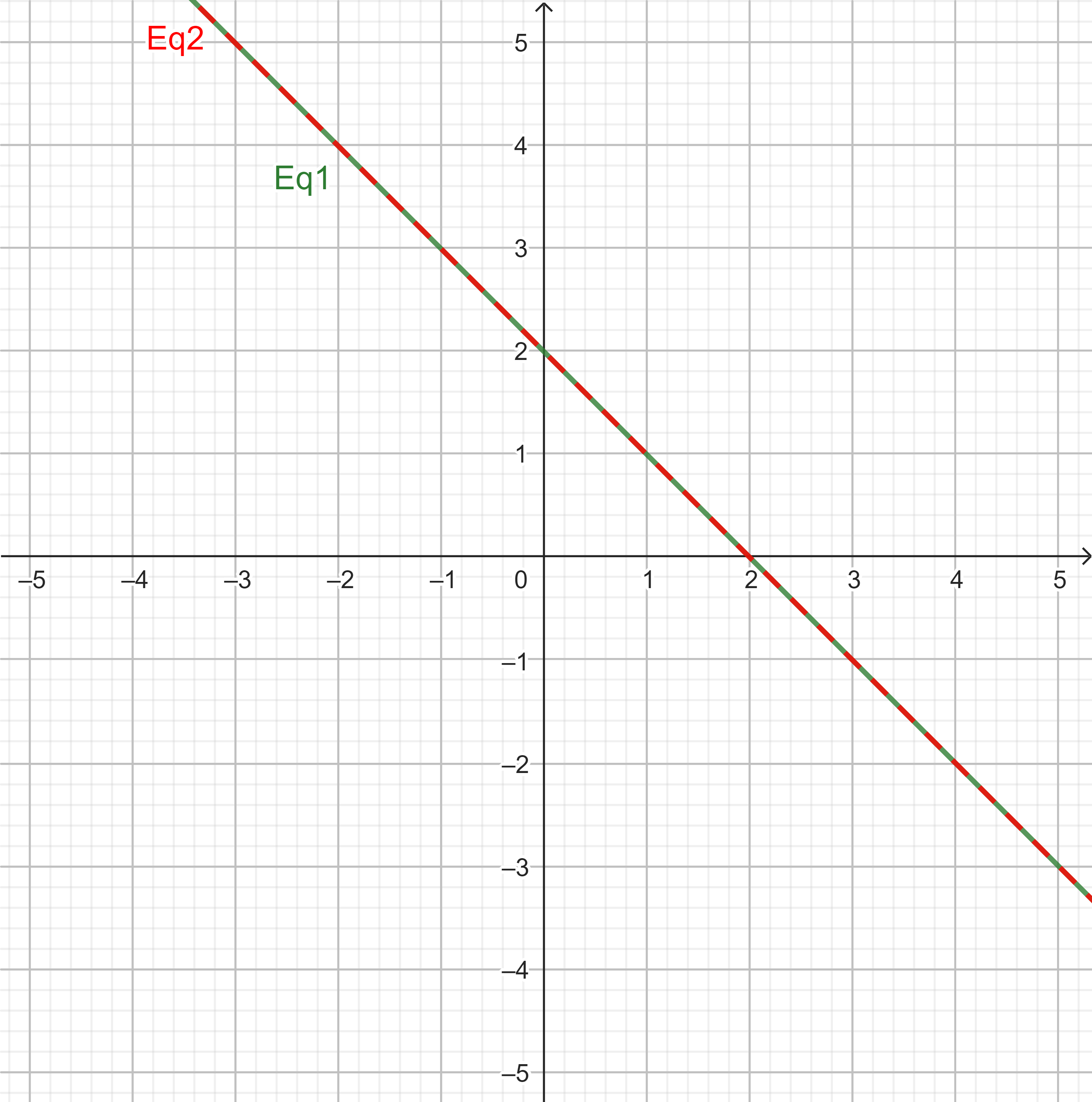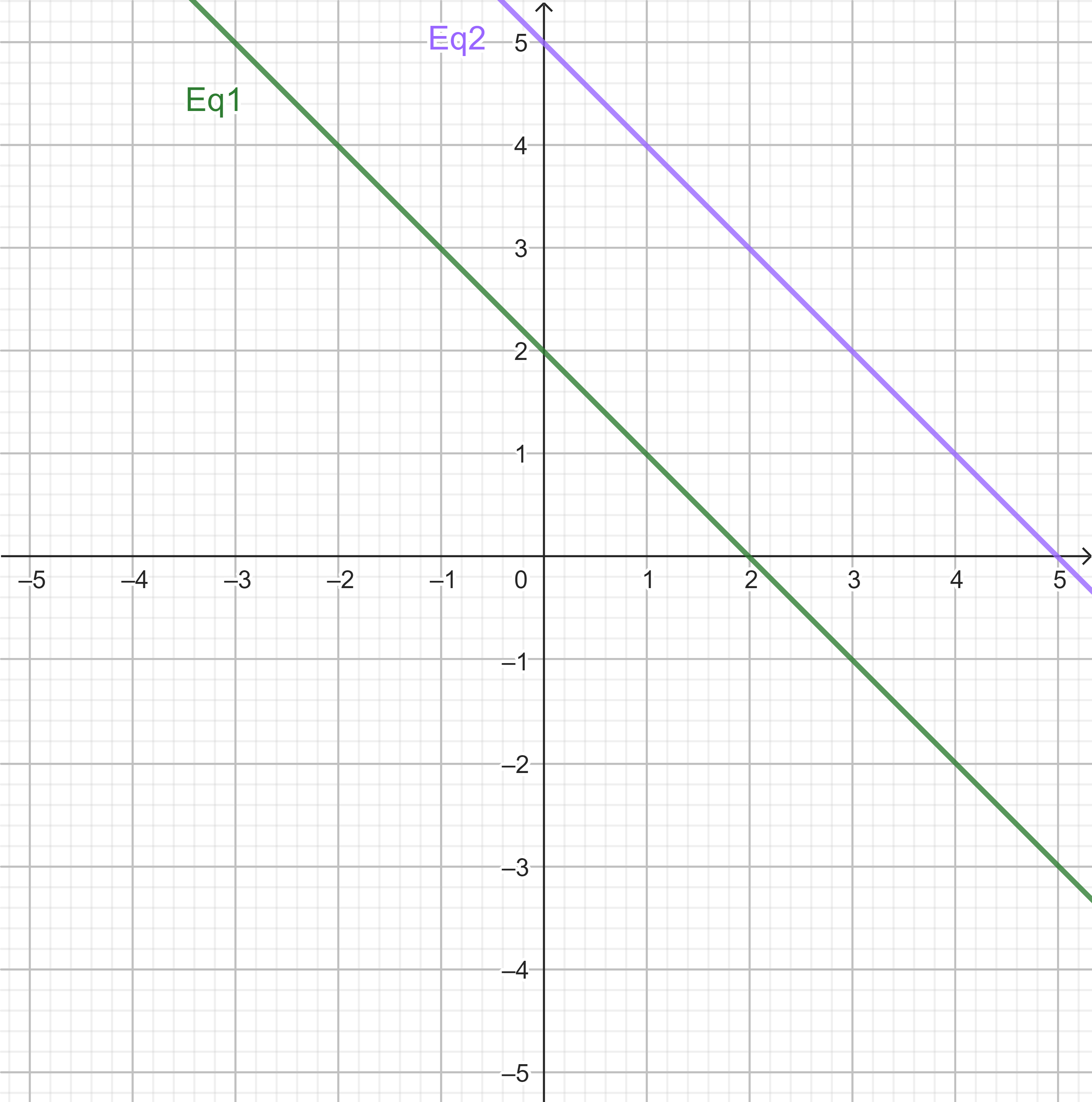Equations \(\begin{aligned}x+y&=2\\10x-y&=-13\end{aligned}\) \(\begin{aligned}x+y&=2\\3x+3y&=6\end{aligned}\) \(\begin{aligned}x+y&=2\\2x+2y&=10\end{aligned}\)
Solution \(x=-1,\;y=3\) Reduces to \(0=0\) Reduces to \(0=±6\)
Description Two lines intersect at (-1, 3) Dependent equations A contradiction
Interpretation Equations are consistent Equations are consistent Equations are inconsistent

Methods for solving a 2 × 2 system of equations

The two main methods for solving simultaneous equations are by:

  1. elimination
  2. substitution.

Elimination method

The elimination method seeks to eliminate (remove) the term containing the same variable from each equation.

Example 1

Solve the following equations simultaneously using the elimination method.

$$\begin{alignat}{2}3x-5y&=2\quad&\mathsf{Equation} (1)\\2x-3y&=4\quad&\mathsf{Equation} (2)\end{alignat}$$

Complete the following activity for a step-by-step guide to solving a 2 × 2 system of equations.

Hence, a unique solution \(x=14\) and \(y=8\) is obtained.

Substitution method

The substitution method uses one equation to substitute (replace) one of the variables in the other equation.

Example 2

Solve the following equations simultaneously using the substitution method.

$$\begin{alignat}{2}y&=3x-1\quad&&\mathsf{Equation} (1)\\x+2y&=12\quad&&\mathsf{Equation} (2)\end{alignat}$$

Step instrucions Calculations
  1. Substitute equation (1) into equation (2).
  2. Expand and collect like terms.
  3. Solve.
 $$\begin{aligned}x+2(3x-1)&=12\\7x&=14\\x&=2\end{aligned}$$
  1. Substitute the \(x{\text-}\)value into either equation and solve for \(y\).
 $$\begin{aligned}y&=3(2)-1\\&=5\end{aligned}$$

Hence, a unique solution \(x=2\) and \(y=5\) is obtained.

Graphing calculators

Using a graphing calculator will help you to visualise how the equations, and the lines they draw, interact. You may have your own graphing calculator or you can use a free online application, such as Desmos or GeoGebra.

In either of the online applications, simply enter the equations from the exercises into the input panel on the left of the window. Make sure you add each equation into a different input block. They will graph automatically, so you can see how the lines interact, or don't!

Exercise 1: 2 × 2 system of equations (unique solution)

Solve the following simultaneous equations:

  1. \(\begin{aligned}2x+3y&=1\\3x-y&=7\\\end{aligned}\)
  2. \(\begin{aligned}x-y&=8\\5x+2y&=61\\\end{aligned}\)
  3. \(\begin{aligned}4x+3y+14&=0\\-5x+2y-29&=0\\\end{aligned}\)
Answers for Exercise 1
  1. \(x=2,\;y=-1\)
  2. \(x=11,\;y=3\)
  3. \(x=-5,\;y=2\)

Exercise 2: 2 × 2 system of equations

Solve the following simultaneous equations. Give the unique solution, if it exists. Otherwise, state whether the equations are dependent or inconsistent.

  1. \(\begin{aligned}x-4y&=-5\\2x+3y&=23\\\end{aligned}\)
  2. \(\begin{aligned}x-y&=8\\5x-5y&=40\\\end{aligned}\)
  3. \(\begin{aligned}4x+2y&=24\\-3x-1.5y&=30\\\end{aligned}\)
  4. \(\begin{aligned}2x+3y&=1\\6x+9y&=3\\\end{aligned}\)
  5. \(\begin{aligned}x-7y&=8\\5x-35y&=61\\\end{aligned}\)
  6. \(\begin{aligned}4x+2y&=22\\-3x-5y&=-27\\\end{aligned}\)
Answers for Exercise 2
  1. Unique solution: \(x=7,\;y=3\)
  2. Infinite number of solutions: Dependent equations (coincident lines)
  3. No solution: Inconsistent equations (parallel lines)
  4. Infinite number of solutions: Dependent equations (coincident lines)
  5. No solution: Inconsistent equations (parallel lines)
  6. Unique solution: \(x=4,\;y=3\)

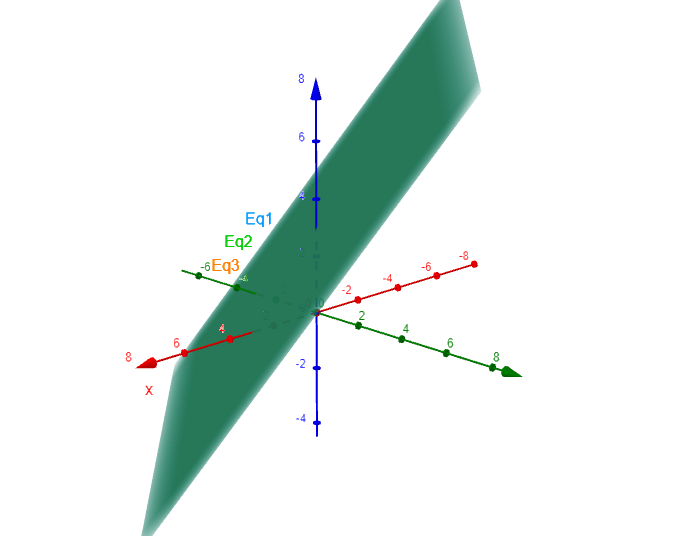
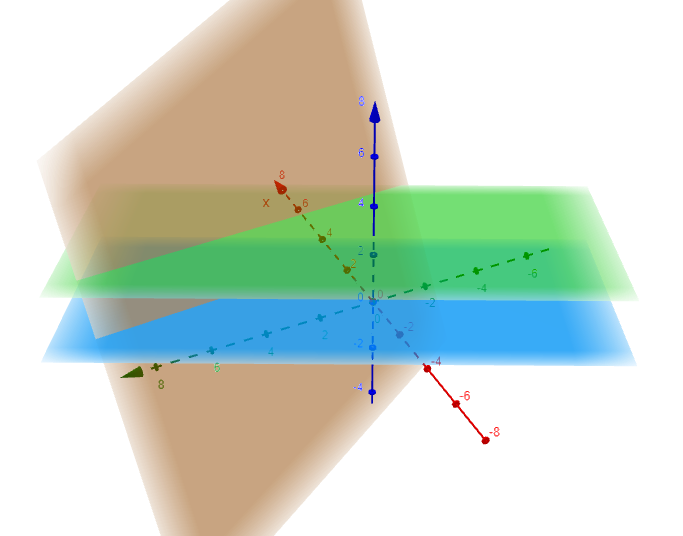
A linear equation with three unknown variables represents a plane in 3-dimensional space (3D for short).

For example, the linear equation \(x+3y+z=3\) represents the plane on the \(xyz{\text-}\)axes shown in the following diagram.

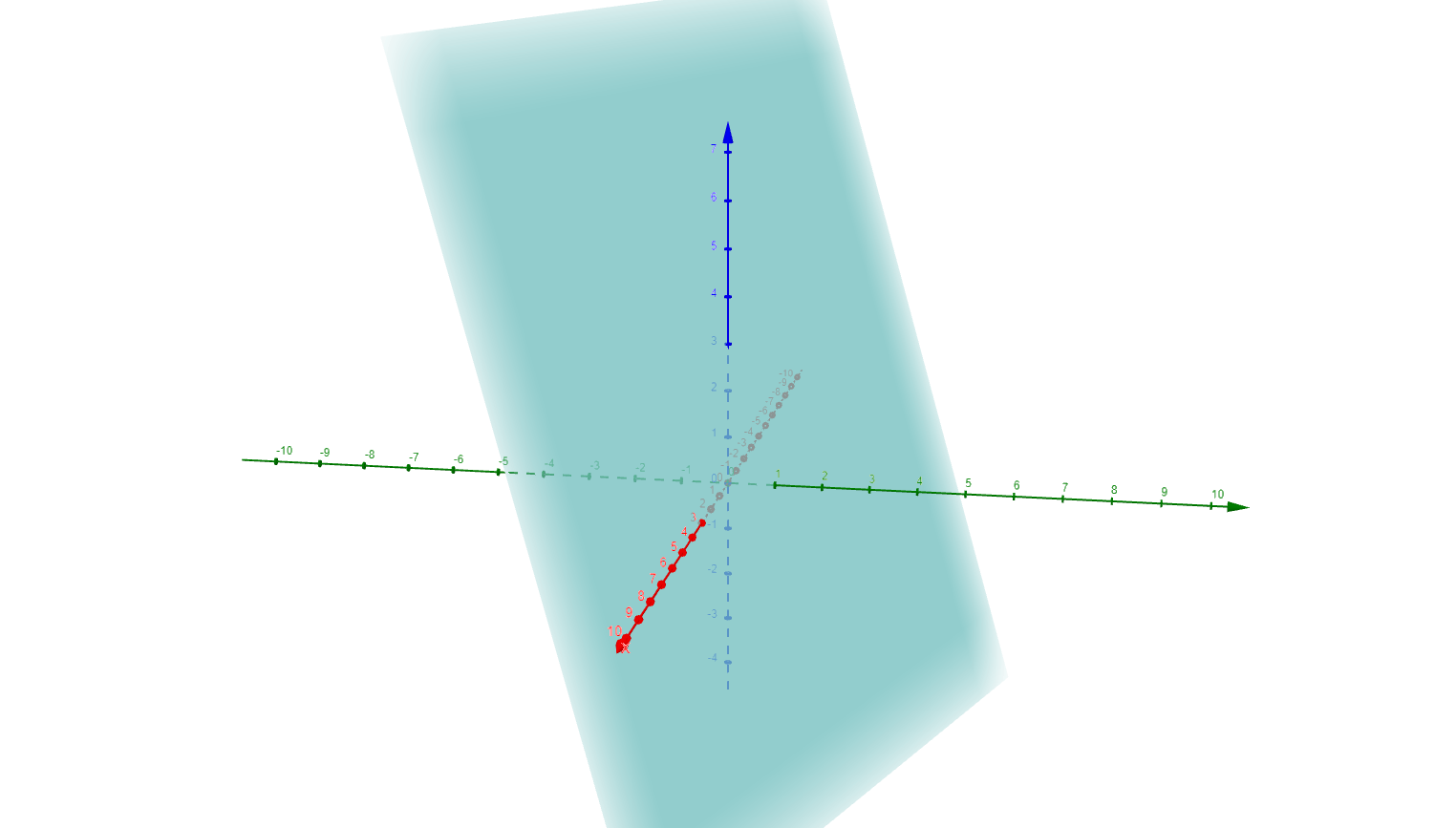
Three linear equations are required to solve equations with three unknown variables. As before, the aim is to obtain a single value for each variable to satisfy each equation simultaneously.

For example, consider the following three simultaneous equations with three unknown variables:

$$\begin{aligned}x+3y-2z&=-8\\2x-y+3z&=19\\5x+2y-z&=9\end{aligned}$$

When solved, \(x=3\), \(y=-1\) and \(z=4\) are obtained.

These values are said to satisfy the three simultaneous equations because they are true for all three equations simultaneously.

Geometric Interpretations - Three Linear Equations with Three Unknowns

As with simultaneously solving two linear equations with two unknowns, there are three possible outcomes when attempting to simultaneously solve three linear equations with three unknown variables:

  1. A unique solution
  2. Multiple solutions
  3. No solution.

Watch the following video to learn about the different ways in which three planes can interact and the number of possible solutions a system of three simultaneous equations can have as a result.

<Break the following video into 2 - part 1 about geometric interpretations, part 2 about methods of solving??>

1. A unique solution

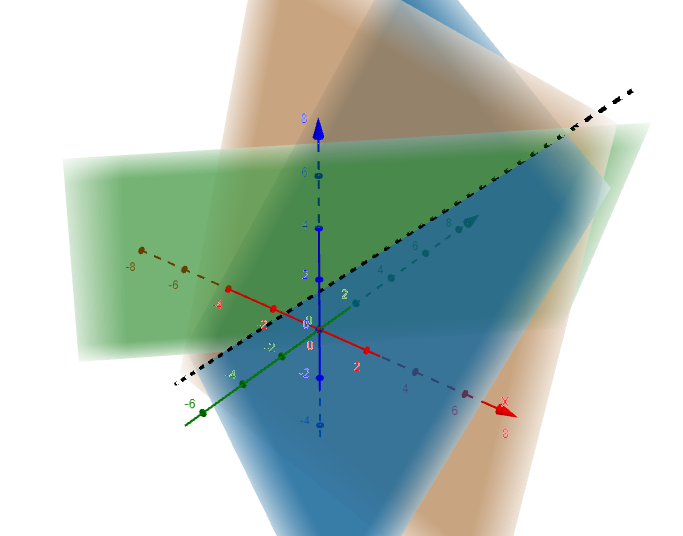
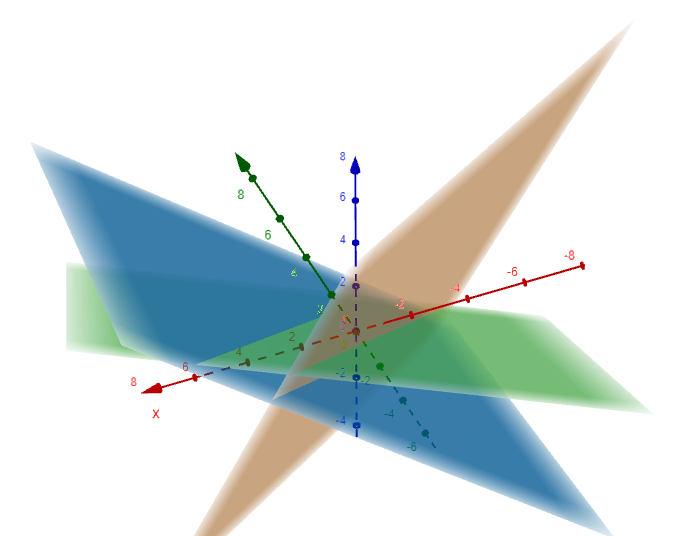
There is one set of values for the unknowns that makes all three equations true because there is a single point where all three planes intersect, as shown in the following diagram. 

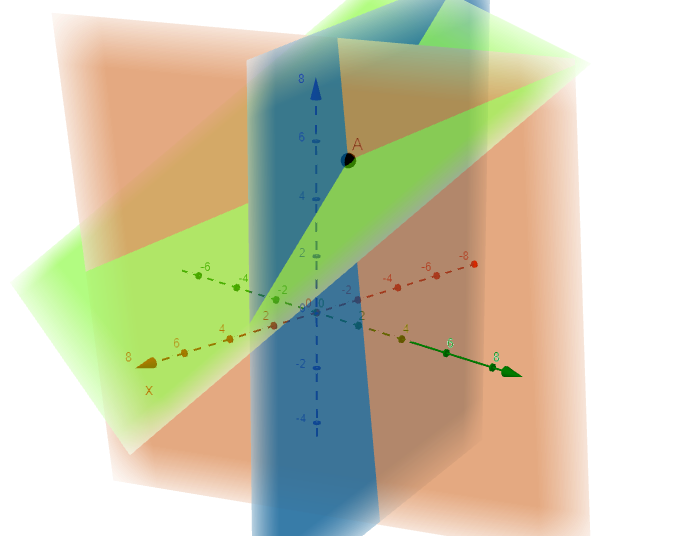
For example, consider the following simultaneous equations.

$$\begin{aligned}x + 3y - 2z &= -8 \\2x - y + 3z &= 19 \\5x + 2y - z &= 9\end{aligned}$$

Solution: \(x=3,\;y=-1,\;x=4\)

Clue: There should be no pattern in the coefficients and constants.

Geometric interpretation: Equations are consistent.

2. Multiple solutions

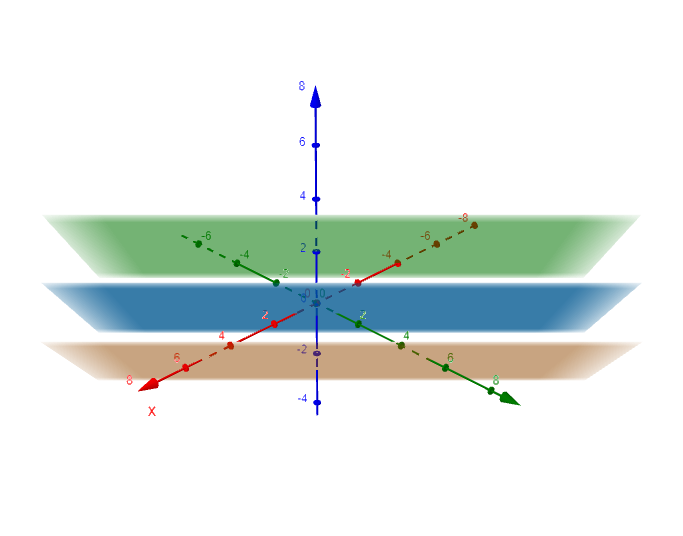
There are two ways a set of three simultaneous linear equations can have multiple solutions. Either all three planes are identical, or all three planes intersect on the same line.

Geometric Interpretation Three Coincident Planes Three Planes Instersecting on a Common Line
Geometric Representation

The three planes completely overlap so that there only looks like there is one plane.

The three planes all cross over at the same line, as shown by the dotted black line.
Example Equations $$\begin{aligned}x-y+z&=3\\2x-2y+2z&=6\\3x-3y+3z&=9\end{aligned}$$ $$\begin{aligned}2x+3y-2z&=5\\-x+y+z&=4\\x+4y-z&=9\end{aligned}$$
Solution

The equations reduce to \(0=0\), so there are multiple solutions.
Description of System of Equations Equations are dependent and consistent.
Clues There is a linear pattern in the coefficients and constants. In this example, equations (2) and (3) are multiples of equation (1). There is a linear pattern in the coefficients and constants.

3. No solution

There are three cases in which three simultaneous linear equations have an outcome of no solutions:

  1. None of the planes intersect at any point
  2. Two planes intersect with the third but not with each other
  3. Each plane intersects at unique points with the others - three separate points of intersection.
Geometric Interpretation Three Parallel Planes Two Parallel Planes with One Intersecting Plane Each Plane is Parallel to the Intersection of the Other Two Planes
Geometric Representation

When all three planes are parallel, they cannot overlap at any point, meaning there is no solution that satisfies all three equations.

When two planes are parallel but are both intersected by the third, there is no point at which all three planes can intersect, so there is no solution that satisfies all three equations.

When each plane intersects with the other two but on a different line, the planes form a triangle. The three planes cannot share one single intersection point, so there is no solution that satisfies all three equations.
Example Equations $$\begin{aligned}x+y-2z&=1\\x+y-2z&=-4\\3x+3y-6z&=16\end{aligned}$$ $$\begin{aligned}2x-y+5z&=3\\2x-y+5z&=14\\3x+2y-z&=12\end{aligned}$$ $$\begin{aligned}2x-3y-3z&=1\\x+y+z&=-6\\3x-2y-2z&=4\end{aligned}$$
Solution The equations reduce to \(0=n\), which is a contradiction.
Description of System of Equations Equations are inconsistent.
Clues

For all three equations:

  • Coefficients of corresponding variables in an equation are a multiple of these in another equation.
  • Constant terms do not follow the same pattern.

One equation is distinct, while for the other two equations:

  • Coefficients of corresponding variables in an equation are a multiple of these in another equation.
  • Constant terms do not follow the same pattern.

One equation is distinct, while for the other two equations:

  • The coefficients of a variable have a simple linear rule.
  • Constant terms do not follow the same pattern.
Check your understanding

Complete the following activity to test your understanding of how to determine the geometric interpretation and, therefore, the number of possible solutions for a given system of three equations with three unknowns.

Methods for solving a 3 × 3 system of equations

You can use elimination or substitution methods to simultaneously solve three linear equations with three unknowns.

The following examples demonstrate using both methods to solve the same system of equations.

Example 3 - Substitution method

This method substitutes (replaces) one variable in two of the equations with the third equation.

For example, solve the following equations simultaneously.

$$\begin{alignat}{2}x+3y-2z&=-8\quad&(1)\\2x-y+3z&=19\quad&(2)\\5x+2y-z&=9\quad&(3)\end{alignat}$$

Step Instructions Calculations
  1. Rearrange equation (1) to make \(x\) the subject.
 $$\begin{aligned}x+3y-2z&=-8\quad&(1)\\x&=-3y+2z-8\quad&(4)\end{aligned}$$
  1. Substitute equation (4) into equations (2) and (3).
  2. Expand and collect like terms.
  3. Simplify.

Note: Equations (5) and (6) now form a system of equations of two linear equations with two unknowns.

 $$\begin{aligned}2(-3y+2z-8)-y+3z&=19\quad&(2)\\-6y+4z-16-y+3z&=19\\-7y+7z&=35\\y-z&=-5\quad&(5)\\\\5(-3y+2z-8)+2y-z&=9\quad&(3)\\-15y+10z-40+2y-z&=9\\-7y+7z&=35\\13y-9z&=-49\quad&(6)\end{aligned}$$
  1. Solve equations (5) and (6) using the substitution or elimination method.
    Using substitution:
    1. Rearrange (5).
    2. Substitute (5) into (6) and solve.
    3. Substitute the value into (5) or (6) and solve for the other unknown.
    4. Substitute known variables into equations (1), (2) or (3) to solve for the final unknown.
 $$\begin{aligned}y-z&=-5\quad&(5)\\y&=z-5\\13(z-5)-9z&=-49\quad&(6)\\z&=4\\\\y-(4)&=-5\quad&(5)\\y&=-1\\\\x+3(-1)-2(4)&=-8\quad&(1)\\x-11&=-8\\x&=3\end{aligned}$$

The unique solution for this system of equations is \(x=3,\;y=-1\;z=4\).

Example 4 - Elimination method

This method aims to eliminate (remove) a term from each equation containing the same variable.

For example, solve the following equations simultaneously.

$$\begin{aligned}x+3y-2z&=-8\quad&(1)\\2x-y+3z&=19\quad&(2)\\5x+2y-z&=9\quad&(3)\end{aligned}$$

Step Instructions Calculations
  1. Decide which variable to eliminate. In this example, \(x\).
  2. Multiply equation (1) by 2.
 $$\begin{aligned}x+3y-2z&=-8\;&(1)\\&\times2\\2x+6y-4z&=-16\;&(4)\end{aligned}$$
  1. Subtract equation (2) from equation (4).
 $$\begin{aligned}2x+6y-4z&=-16\;&(4)\\- 2x-y+3z&=19\;&(2)\\7y-7z&=-35\\y-z&=-5\;&(5)\end{aligned}$$
  1. Multiply equation (1) by 5.
 $$\begin{aligned}x+3y-2z&=-8\;&(1)\\&\times5\\5x+15y-10z&=-40\;&(6)\end{aligned}$$

 

  1. Subtract equation (3) from equation (6).

 

Note: Equations (5) and (7) now form a system of equations of two linear equations with two unknowns.

 $$\begin{aligned}5x+15y-10z&=-40\;&(6)\\- 5x+2y-z&=9\;&(3)\\13y-9z&=-49\;&(7)\end{aligned}$$
  1. Solve equations (5) and (7) using the substitution or elimination method.
    Using elimination:
    1. Multiply equation (5) by 13.
    2. Subtract equation (7) from equation (8) and solve.
    3. Substitute the known value into (5) and solve for the other unknown.
    4. Substitute known variables into equations (1), (2) or (3) to solve for the final unknown.
 $$\begin{aligned}y-z&=-5\;&(5)\\&\times13\\13y-13z&=-65\;&(8)\\- 13y-9z&=-49\;&(7)\\z&=4\\\\y-(4)&=-5\;&(5)\\y&=-1\\\\2x-(-1)+3(4)&=19\;&(2)\\2x+1+12&=19\\x&=3\end{aligned}$$

The unique solution for this system of equations is still \(x=3,\;y=-1\;z=4\).

You may like to use the GeoGebra 3D Graphic Calculator to help you solve the following exercises. Enter the equations from the exercises into the input panel on the left of the window to see how the planes interact. Add each equation into a different input block. The equations from the first question have been entered for you, but you can edit the equations to be whatever you like.

Once you have drawn all three planes, select and drag the graphic representation around to see the planes from all angles and to see if or where they intersect.

Exercise 3: 3 × 3 system of equations (unique solution)

Solve the following simultaneous equations:

  1. \(\begin{aligned}2x-2y+z&=13\\3x+y+3z&=17\\2x+3y-2z&=5\\\end{aligned}\)
  2. \(\begin{aligned}-2x+y+z&=-5\\4x-y+3z&=10\\2x-2y+2z&=13\\\end{aligned}\)
  3. \(\begin{aligned}3x+5y+3z&=2\\-x-y+5z&=10\\2x+y+z&=4\\\end{aligned}\)
Answers for Exercise 3
  1. \(x=1,\;y=3,\;z=2\)
  2. \(x=5,\;y=-1,\;z=1\)
  3. \(x=7,\;y=3,\;z=2\)
  4. \(x=0.5,\;y=-5,\;z=1\)
  5. \(x=7,\;y=1,\;z=-3\)
  6. \(x=2,\;y=-2,\;z=2\)

Exercise 4: 3 × 3 system of equations

Solve the following simultaneous equations. Give the unique solution, if it exists. Otherwise, state whether the equations are dependent or inconsistent. For each system of equations, provide a geometric interpretation.

  1. \(\begin{aligned}x+4y-z&=3\\-2x-8y+2z&=-6\\3x+12y-3z&=9\\\end{aligned}\)
  2. \(\begin{aligned}3x-2y-2z&=4\\7x+y-z&=8\\10x-y-3z&=10\\\end{aligned}\)
  3. \(\begin{aligned}x-5y-3z&=23\\2x+2y+3z&=26\\3x-15y-9z&=65\\\end{aligned}\)
Answers for Exercise 4
  1. Unique solution: \(x=1,\;y=2,\;z=3\)
  2. Multiple solutions: Dependent equations forming three coincident planes.
  3. No solution: Inconsistent equations forming three parallel planes.
  4. No solution: Inconsistent equations forming three planes, where each plane is parallel to the intersection of the other two planes.
  5. Unique solution: \(x=0,\;y=5,\;z=3\)
  6. No solution: Inconsistent equations forming two parallel planes and one intersecting plane.

To form a system of equations to solve simultaneously, use the following steps:

  1. Carefully read the information provided.
  2. Organise the provided information into 'sets of information'.
  3. Identify the variables and assign them appropriate pronumerals.
  4. Form an equation for each set of information.

The following video introduces how to model situations with systems of equations.

Example 5 – Forming a 2×2 system of equations

It takes a swimmer 42 minutes to swim 6 laps of freestyle and 10 laps of breaststroke. It takes the same swimmer 40 minutes to swim 8 laps of freestyle and 8 laps of breaststroke.

Form two equations to represent this information.

Step Instructions Calculations
1. Identify the sets of information provided in the scenario.
  • 6 laps of freestyle and 10 laps of breaststroke takes 42 minutes.
  • 8 laps of freestyle and 8laps of breaststroke takes 40 minutes.
2. Choose pronumerals to represent the variables and convert the sets of information into equations.

Let \(f\) represent the time taken to swim a lap of freestyle and \(b\) represent the time to swim one lap of breaststroke.

  • 6 laps of freestyle and 10 laps of breaststroke takes 42 minutes.
    • \(6f+10b=42\)
  • 8 laps of freestyle and 8laps of breaststroke takes 40 minutes.
    • \(8f+8b=40\)
Example 6 – Forming a 3×3 system of equations

Three burgers, two servings of fries and three soft drinks cost $75. Four burgers and four soft drinks have a total cost of $84. A burger and a serving of fries cost $22.

Form a system of equations to represent this information.

Step Instructions Calculations
1. Identify the sets of information provided in the scenario.
  • 3 burgers, 2 servings of fries and 3 soft drinks cost $75.
  • 4 burgers and 4 soft drinks have a total cost of $84.
  • 1 burger and 1 serving of fries cost $22.
2. Choose pronumerals to represent the variables and convert the sets of information into equations.

Let \(b\) represent the number of burgers, \(f\) represent the servings of fires and \(d\) represent the number of soft drinks.

  • 3 burgers, 2 servings of fries and 3 soft drinks cost $75.
    • \(3b+2f+3d=75\)
  • 4 burgers and 4 soft drinks have a total cost of $84.
    • \(4b+4d=84\)
  • 1 burger and 1 serving of fries cost $22.
    • \(1b+1f=22\)
Check your understanding

Now that you have looked at a few examples, let's try one together.

Exercise 5: Writing systems of equations

Question 1

A forester plans to plant a forest with three types of trees (\(A\), \(B\), and \(C\)). Tree \(A\) costs $30 per tree, tree \(B\) costs $10 per tree, and tree \(C\) costs $40 per tree. The forest needs a total of 75 trees at a total cost of $1000.

The number of type \(B\) trees to be bought is the same as the combined total of the numbers of type \(A\) trees and twice the number of type \(C\) trees.

Set up a system of 3 equations for this information. Do not solve the equations.

\(\begin{aligned}A + B + C &= 75\\A – B + 2C &= 0\\30A + 10B + 40C &= 1000\end{aligned}\)

Question 2

In Rugby, there are three main ways of scoring points:

  • Try - 5 points
  • Conversion - 2 points
  • Penalty - 3 points.

Let \(T\) be the number of Tries scored, \(C\) the number of Conversions scored, and \(P\) the number of Penalties scored by a team in a game.

  • The team scores 54 points in a game.
  • They score two fewer Conversions than Tries in the game.
  • The total number of Tries and Conversions is four times the number of Penalties.

Set up a system of 3 equations for this information. Do not solve the equations.

\(\begin{aligned}5T + 2C + 3P &= 54\\T − C &= 2\\4P &= T + C\end{aligned}\)

Question 3

In a season, the Celtic Football Club draws four more games than it loses. The Celtic Football Club gains 82 points, where a win is awarded 3 points, a draw 1 point and a loss 0 points. The team wins 50% more games than the combined number it draws and loses.

Write down 3 equations using this information.

Solve the equations to find out how many games Celtic Football Club played in the season.

\(\begin{aligned}D – L &= 4\\3W + D &= 82\\W = 1.5 (D + L)\end{aligned}\)

40 games.

Question 4

The number of students studying Economics (\(E\)) is 42 less than the number of Chemistry students (\(C\)) and the number of Statistics students (\(S\)) together. The mean number of students studying Economics, Chemistry and Statistics is 96. The number of Economics students is nine fewer than the number of Statistics students.

Set up 3 equations from this information. Do not solve the equations.

\(\begin{aligned}E &= C + S – 42\\\frac{C+S+E}{3}&=96\\S – E&= 9 \end{aligned}\)

Question 5

The number of students at the school studying Accounting is \(A\), the number studying Physics \(P\), and the number studying Statistics is \(S\). Construct 3 equations using the following information in terms of \(A\), \(P\) and \(S\). Do not solve the equations.

The mean number of students studying Accounting, Physics and Statistics at a school is 80. The total number of Accounting and Physics students together equals 60% of the number of Statistics students. The number of Accounting students exceeds the number of Physics students by 28.

\(\begin{aligned}\frac{A + P + S}{3}&=80\\A + P &= 0.6S\\A& = P + 28 \end{aligned}\)

Understanding the possible outcomes when attempting to solve simultaneous equations and what constitutes consistent and inconsistent equations allows us to answer questions in which a constant and/or a coefficient in one of the equations is undefined.

Example 7 – 2×2 Inconsistent equations

Find a value for \(k\) for which the following system of linear equations is inconsistent.

$$\begin{aligned}2x+3y&=9\quad&(1)\\4x+ky&=30\quad&(2)\end{aligned}$$

Step Instructions Calculations
  1. For inconsistent equations, we expect the system of equations to reduce to \(0=n\).
    This can be obtained by multiplying equation (1) by 2 to obtain equation (3).
 $$\begin{alignat*}{6}2x&+&3y&=&9\quad&(1)&\times2\\4x&+&6y&=&18\quad&(3)&\end{alignat*}$$
  1. Subtract equation (3) from equation (2).
 $$\begin{alignat*}{4}4x+ky&=&30\quad&(2)&\\4x+6y&=&18\quad&(3)&\\\\0+(k-6)y&=&12\quad&(2)-(3)&\end{alignat*}$$

Hence, \(k\) must equal 6 to ensure that equation (4) reduces \(0=n\).

Example 8 – 2×2 Consistent (dependent) equations

Find a value for \(k\) and \(C\) for which the following system of linear equations is dependent.

$$\begin{aligned}2x+3y&=9\quad&(1)\\4x+ky&=C\quad&(2)\end{aligned}$$

Step Instructions Calculations
  1. For dependent equations, we expect the system of equations to reduce to \(0=0\).
    This can be obtained by multiplying equation (1) by 2 to obtain equation (3).

$$\begin{alignat*}{3}2x+3y&=&9\quad&(1)\times2\\4x+6y&=&18\quad&(3)\end{alignat*}$$
  1. Subtract equation (3) from equation (2).
 $$\begin{alignat*}{2} 4x + ky &= C \quad &&(2) \\ 4x + ky &= 18 \quad &&(3) \\ 0 + (k - 6)y &= C - 18 \quad &&(2) - (3) \end{alignat*}$$

Hence, \(k\) must equal 6 and \(C\) must equal 18 to ensure that equation (4) reduces \(0=0\).

Example 9 – 3×3 Inconsistent equations

Find a value for \(A\), \(B\) and \(C\) for which the following system of linear equations is inconsistent.

$$\begin{aligned}-3x+2y+z&=-6\quad&(1)\\ x-3y+2z&=-5\quad&(2)\\ 2x+Ay+Bz&=C\quad&(3)\end{aligned}$$

Step Instructions Calculations
  1. For inconsistent equations, we expect the system of equations to reduce to \(0=n\).
    To do this, eliminate the \(x\) term:
    1. Multiply equation (2) by 3.
    2. Add to equation (1).
    3. Simplify.
 $$\begin{alignat*}{3}3x-9y+6z&=&-15\quad&(2)\times3\\-3x+2y+z&=&-6\quad&(1)\\\\0x-7y+7z&=&-21\quad&(2)\times3+(1)\\-y+z&=&-3\quad&(4)\end{alignat*}$$
  1. Eliminate the \(x\) term:
    1. Multiply equation (2) by -2.
    2. Add to equation (3).
 $$\begin{alignat*}{2}-2x+6y-4z&=10\quad&&(2)\times-2\\2x+Ay+Bz&=C\quad&&(3)\\\\-2x+2x+6y+Ay-4z+Bz&=C+10\quad&&(2)\times-2+(3)\\(6+A)y+(B-4)z&=C+10\quad&&(5)\end{alignat*}$$
  1. Consider equations (4) and (5). For inconsistent equations, we need equations (4) and (5) to reduce to \(0=n\). Equate the \(y\) and \(z\) coefficients and the constant terms.

$$\begin{alignat*}{3}-y+z&=&-3\quad&\quad(4)\\(6+A)y+(B-4)z&=&\,C+10&\quad(5)\end{alignat*}$$

$$\begin{alignat*}{3} y\mathsf{{\text -}variable}:\quad-1&=\,A+6&\Rightarrow\,A&=-7\\z\mathsf{{\text -}variable}:\quad1&=\,B-4&\Rightarrow\,B&=\;5\\\mathsf{constants}:\quad-3&\neq\,C+10&\Rightarrow\,C&\neq-13\end{alignat*}$$
Example 10 – 3×3 Consistent (dependent) Equations

Find a value for each of \(A\), \(B\) and \(C\) for which the following system of linear equations is dependent.

$$\begin{alignat*}{3}-3x + 2y + z &=& -6\quad &(1)\\x - 3y + 2z &=& -5\quad &(2)\\2x + Ay + Bz &=& C\quad &(3)\end{alignat*}$$

Step Instructions Calculations
  1. For dependent equations, we expect the system of equations to reduce to \(0 = 0\). To do this, eliminate the \(x\) term:
    1. Multiply equation (2) by 3.
    2. Add to equation (1).
    3. Simplify.
 $$\begin{alignat*}{2}3x - 9y + 6z &= -15 \quad &&(2)\times3 \\ -3x + 2y + z &= -6 \quad&&(1) \\ 0x - 7y + 7z &= -21 \quad && \\ - y + z &= -3 \quad &&(4) \end{alignat*}$$
  1. Eliminate the \(x\) term:
    1. Multiply equation (2) by -2.
    2. Add to equation (3).
    3. Simplify.
 $$\begin{alignat*}{2} -2x + 6y - 4z &= 10 \quad&& (2)\times2\\ 2x + Ay + Bz &= C \quad &&(3) \\0x+6y+Ay+Bz-4z&=C\quad&&\\ (6 + A) y + (B - 4) z &= C + 10 \quad &&(5) \end{alignat*}$$
  1. Consider equations (4) and (5). For dependent equations, we need equations (4) and (5) to reduce to \(0=0\). Equate the \(y\) and \(z\) coefficients and the constant terms.

$$\begin{alignat*}{2}-y+z&=-3\quad&\quad(4)\\(6+A)y+(B-4)z&=C+10&\quad(5)\end{alignat*}$$

$$\begin{alignat*}{4} &y\mathsf{{\text -}variable}:\quad-1&=\;A+6&\Rightarrow\;A&=-7\\&z\mathsf{{\text -}variable}:\quad\;1&=\;B-4&\Rightarrow\;B&=\;5\\&\mathsf{constants}:\quad-3&\neq\;C+10&\Rightarrow\;C&\neq-13\end{alignat*}$$
Example 11 – 3×3 Consistent (dependent) Equations: A General Case

Find a range of values for each of \(A\), \(B\) and \(C\) for which the following system of linear equations is dependent.

$$\begin{alignat*}{3}-3x + 2y + z &=& -6\quad &(1)\\x - 3y + 2z &=& -5\quad &(2)\\2x + Ay + Bz &=& C\quad &(3)\end{alignat*}$$

Note: These are the same equations as in Example 11. The only difference is that a range of values (general case) for \(A\), \(B\) and \(C\) are required.

Initially, the approach to this problem is identical to that in Example 11. However, in this instance, we do not equate the \(y\) and \(z\) coefficients and the constants as we did in Example 11. Instead, we look at the proportions. More specifically, we seek to maintain the proportion for the \(y\) and \(z\) coefficients and the constants between equations (4) and (5).

Step Instructions Calculations
  1. Eliminate \(x\) from equations (1), (2) and (3).
  2. Consider equations (4) and (5).
 $$\begin{alignat*}{2}-y+z&=-3\quad&\quad(4)\\(6+A)y+(B-4)z&=C+10&\quad(5)\end{alignat*}$$
  1. Maintain the proportions of the \(y\) and \(z\) coefficients in equations (4) and (5).
 $$\begin{aligned} \frac{-1}{A + 6} &= \frac{1}{B - 4} \\ 4 - B &= A + 6 \\\\ \mathsf{Let}\; A = m, \quad 4 - B &= m + 6 \\ \mathsf{Hence,}\quad B &= -2 - m \end{aligned}$$
  1. Similarly, maintain the proportions of the \(y\) and the constants in equation (4) and (5).
 $$\begin{aligned}\frac{-1}{A + 6} &= \frac{-3}{C+10} \\-10-C &= -3A - 18 \\\\ \mathsf{Let}\; A = m, \quad -10-C &= -3m - 18 \\ \mathsf{Hence,}\quad C &= 3m+8 \end{aligned}$$
  1. State the general solution.
 $$A = m,\;B = -2 – m,\;C = 3m +8$$

Alternatively, we could have let \(B\) or \(C\) equal \(m\) and then the other two would have been defined accordingly.

Note: Other approaches to solving this type of question exist.

Example 12 – 3×3 Consistent (dependent) Equations: A General Solution
Additional knowledge

Note: This is additional knowledge. No general formulae will be tested or examined.

In Example 12, a range of values for some undefined coefficients and constants were found. In this example, the aim is to find a general solution for \(x\), \(y\) and \(z\).

Three planes have a common line of intersection, as shown in the following diagram. This leads to multiple solutions - all the points along a common line.

$$\begin{alignat*}{2} x + y + 3z &= 4 \quad &(1) \\ 2x - y - z &= 7 \quad &(2) \\ x - 2y - 4z &= 3 \quad &(3) \end{alignat*}$$

Step Instructions Calculations
  1. Subtract Equation (3) from Equation (1).
  2. Multiply equation (1) by 2, then subtract equation (2).
  3. Subtract equation (5) from equation (4).
 $$\begin{aligned}(1)-(3)\\3y+7z&=1\quad(4)\\2\times(1)-(2)\\3y+7z&=1\quad(5)\\(4)-(5)\\0&=0\end{aligned}$$
  1. One approach is to let \(z=k\). Then, substitute \(z=k\) into either equation (4) or (5) and rearrange to make \(y\) the subject.
 $$\begin{alignat*}{2}3y+7z&=1\quad&(4)\\3y+7k&=1\\3y&=1-7k\\y&=\frac{1}{3}-\frac{7}{3}k\quad&(6)\end{alignat*}$$
  1. Substitute \(y\) from equation (6) into equation (1) and rearrange to make \(x\) the subject.
 $$\begin{alignat*}{2} x + y + 3k &= 4 \quad &(1) \\ x + (\frac{1}{3}-\frac{7}{3}k) + 3k &= 4\\x&=\frac{11}{3}-\frac{2}{3}k\end{alignat*}$$
  1. State the general solution.
 $$\frac{11}{3}-\frac{2}{3}k,\;\frac{1}{3}-\frac{7}{3}k,\;k$$

Exercise 6: Use all your simultaneous equations skills

Question 1

Solve the following systems of equations.

  1. \(\begin{aligned}4x + y - 2z& = -18\\5x + 5y + 5z &= 0\\-2x - 3y &= 14\end{aligned}\)
  2. \(\begin{aligned}6x + 3y + 7z &= 77\\6x + 3y + 7z& = 77\\ + 11 &= 3x + z\end{aligned}\)
  3. \(\begin{aligned}2x + 2y + 2z &= 44\\3y& = 3x + 3z\\15x + 24y + 45z &= 519\end{aligned}\)
  4. \(\begin{aligned}x + y + z& = 123\\x &= 2(y + z)\\3z&= 3y + 15\end{aligned}\)
  1. \(\begin{aligned}A+B+C&=75\\A-B+2C&=0\\30A+10B+40C&=1000\end{aligned}\)
  2. \(\begin{aligned}5T+2C+3P&=54\\T-C&=2\\4P&=T+C\end{aligned}\)
  3. \(\begin{aligned}D-L&=4\\3W+D&=82\\W&=1.5(D+L)\end{aligned}\)
    40 games
  4. \(\begin{aligned}E&=C+S-42\\\frac{C+S+E}{3}&=96\\S-E&=9\end{aligned}\)
  5. \(\begin{aligned}\frac{A+P+S}{3}&=80\\A+P&=0.6S\\A&=P+28\end{aligned}\)
Question 2

A bakery sells three types of products: Cakes, Breads and Savoury snacks.

In a particular month, a total of $100 000 worth of product is sold. Cakes sell $1600 more than Breads and Savoury snacks combined. Breads sell twice as much as Savoury snacks.

  1. Set up and solve a system of equations.
  2. Find the sales of each of the three products sold in a particular month.

\(\begin{aligned}C + B + S &= 100 000\\C &= B + S + 1600\\B &= 2S\end{aligned}\)

Solution: \(C = $50 800; B = $32 800; S = $16 400\)

Question 3

The following set of simultaneous equations has no solutions.

$$\begin{aligned}x - 2y + z&= 2\\x + 3y + 2z& = 3\\3x - y + 4z&= 8\end{aligned}$$

Explain geometrically how the planes represented by these equations are related.

Each plane is parallel to the intersection of the other two planes.

Question 4

Xiao and Yongshan are students who work part time after school. Xiao gets $1.50 more per hour than Yongshan. Xiao works for 8 hours in a week, Yongshan works for 9 hours and together they earn $241.50.

Write a set of simultaneous equations to find the hourly rate of pay for each student. Do not solve the equations.

Let Xiao’s hourly rate be \(x\), let Yongshan’s hourly rate be \(y\)

\(\begin{aligned}x – y &= 1.5\\8x + 9y &= 241.5\end{aligned}\)

Question 5

Thomas has a collection of 75 banknotes of three denominations: $50, $20, and $10. The value of his $50 notes is the same as the value of all the other notes. The number of $50 notes he has is \(\frac{3}{4}\) the number of $10 notes in his collection.

Form and solve a set of simultaneous equations to find if Thomas has enough money to buy a laptop computer with a sale price of $1999, using the banknotes.

Steps Calculations
  1. Let \(x\) represent number of $50, \(y\) the number of $20 and \(z\) the number of $10.
 $$\begin{alignat*}{2}x + y + z &= 75\quad&&(1)\\5x – 2y –z &= 0\quad&&(2)\\x&=\frac{3}{4}z\quad&&(3)\end{alignat*}$$
  1. Substitute (3) into (1):
 $$\begin{aligned}\frac{3}{4}z+y+z&=75\\y+\frac{7}{4}z&=75\quad(4)\end{aligned}$$
  1. Substitute (3) into (2):
 $$\begin{aligned}5(\frac{3}{4})z-2y-z&=0\\-2y+\frac{11}{4}z&=0\quad(5)\\\\\frac{14}{4}z+\frac{11}{4}z&=150\quad2\times(4)+(5)\\25z&=600\end{aligned}$$
Solution: Thomas has $1800, which is not enough to buy the laptop. $$x = 18;\;y = 33;\;z = 24$$
Question 6

Jack makes and sells three different cocktails. He kept a record of his sales over three days. On the first day, he spent a total of 145 minutes making cocktails, on the second day, 130 minutes, and on the third day, he spent two hours making cocktails.

  Number of each cocktail sold
  Day 1 Day 2 Day 3
Fruit Punch 8 2 5
Key Lime 3 2 0
Beach 6 10 8

Set up and solve a system of equations to find out which cocktail takes the longest to prepare.

Let \(a\) be Fruit Punch; \(b\) be Key Lime and \(c\) Beach Sunrise.

\(\begin{aligned}8a + 3b + 6c &= 145\\2a + 2b + 10c &= 130\\5a + 8c &= 120\end{aligned}\)

\(a=\) 8 minutes; \(b=\) 7 minutes; \(c=\) 10 minutes

Beach Sunrise takes the longest to prepare.

Question 7

Consider the following set of equations.

$$\begin{aligned}3x - 6y - 15z &= 18\\x + 4y - 6z &= 18\\-2x + 4y + 10z &= 18\end{aligned}$$

  1. From the following options, how many solutions does this set of equations have?
    1. None
    2. One
    3. Many
  2. Explain geometrically how the planes represented by these equations are related.
  1. A - None
  2. The first and the third planes are parallel.
Question 8

Consider the following system of equations.

$$\begin{aligned}x + y + z &= 3\\2x - 3y + 3z &= 7\\3x - 2y + 4z &= 6\end{aligned}$$

Give a geometrical description of how the planes represented by these three equations relate to each other.

The three planes form a triangular prism, the intersection of two of the planes is parallel to the third.
OR
The three planes do not all intersect at a common point or line, and none are parallel.

Question 9

Consider the following three equations.

$$\begin{aligned}2x - y + 3z &= 4\\x - 2y + 4z& = 7\\Px + Qy + z &= -2\end{aligned}$$

If \(x = 3, y = -10, z = -4\) is a solution, find possible values for \(P\) and \(Q\) that make this solution true.

\(3P – 10Q = 2\), so one possible solution is \(P = 4\) and \(Q = 1\).

Alternatively, let \(P = k, Q = \frac{3k-2}{10}\).

Question 10

Consider the following system of three equations.

$$\begin{alignat*}{2}2x - y + 3z &= 4\quad&(1)\\x - 2y + 4z &= 7\quad&(2)\\4x + y + z &= -2\quad&(3)\end{alignat*}$$

Cathy states a solution is: \(x = 3, y = -10, z = -4\).

Susie states a solution is: \(x = -1, y = 0, z = 2\).

  1. Justify whether Cathy has obtained a correct solution.
  2. Hank thinks there are infinitely many solutions.
    Justify, using algebra, that there are an infinite number of solutions.
  1. Cathy is correct, \(x = 3,y = -10,z = -4\) is a solution to the system of equations. Verify by substituting the values for \(x,y\) and \(z\) into the equations (1), (2) and (3).

    \(\begin{aligned}2(3) – (0) + 3(-4)& = 4\quad&(1)\\(3) – 2(0) + 4(-4) &= 7\quad&(2)\\4(3) + (0) + (-4) &= -2\quad&(3)\end{aligned}\)
  2. Note: There are several correct solutions to this problem. The following is only one example.
    System of equations:

    \(\begin{alignat*}{2} 2x - y + 3z &= 4 \quad &&(1) \\ x - 2y + 4z &= 7 \quad &&(2) \\ 4x + y + z &= -2 \quad &&(3) \\ (1) - (2) \times 2 \quad \quad 3y - 5z &= -10 \quad &&(4) \\ 4 \times (2) - (3) \quad \quad -9y + 15z &= 30 \quad &&(5) \\ -3 \times (4) - (5) \quad \quad 0 &= 0 \quad \Rightarrow \quad \mathsf{infinitely\;many\;solutions} \end{alignat*}\)
Question 11

The following system of equations is dependent.

$$\begin{alignat*}{2}2x + 5y - 3z& = 16\quad&(1)\\3x + y - 2z &= 50\quad&(2)\\-x + 4y + mz& = n\quad&(3)\end{alignat*}$$

  1. State the values of the constants \(m\) and \(n\) that make this true.
  2. Explain what this means geometrically if this system of equations is dependent.
  1. \(m = -1,\;n = -34\)
  2. The three planes meet along a common line.
Question 12

Consider the following system of three equations in \(x, y,\) and \(z\).

$$\begin{aligned}10x + 3y + 4z &= 18\\-2x + y - 2z &= 12\\px + 3y - z&= q\end{aligned}$$

Give values for \(p\) and \(q\) in the third equation, which makes this system dependent.

Eliminate \(z\)

\(\begin{alignat*}{2}6x + 5y &= 42 \quad \quad&&(1)+(2)\times2\\(2p + 2)x + 5y &= 2q - 12\quad \quad &&2\times(3)-(2)\end{alignat*}\)

For the set of equations to be dependent: \(\frac{2p+2}{6}=\frac{5}{5}=\frac{2q-12}{42}\)

So, \(p=2,\;q=27\).

Question 13

Find the two values of \(k\) for which the following pair of equations has no solution.

$$\begin{aligned}x + ky &= 4\\(k+3)x - 2y &= 6\end{aligned}$$

The lines must be parallel and not coincident, so the ratios of the coefficients must be:

\(\frac{1}{k+3}=\frac{k}{-2}\neq\frac{4}{6}\;\Rightarrow\;k(k+3)= -2\;\Rightarrow\;k^2 + 3k + 2 = 0\)

\((k + 1)(k + 2) = 0\) so \(k = -1,-2\).

Question 14

Find the value of \(k\) for which the system of equations has a unique solution.

$$\begin{aligned}7x + 7y &= 7\\x + ky &= 2\\kx + y& = 3\end{aligned}$$

Adding equations (2) and (3): \((k + 1)x + (k + 1)y = 5\).

For the set of equations to be consistent: \(\frac{1}{k+1}=\frac{1}{k+1}=\frac{1}{5}\)

\(k+1=5\) so \(k=4\).

Question 15

A plane has the points (1, 1, 1), (2, 2, 0), (\(\frac{1}{3}\), 1, 2) on it.

Find \(A, B\) and \(C\) if the equation of the plane is \(Ax + By + Cz = 4\). Show your working.

\(\begin{alignat*}{2}A+B+C&=4\quad&&(1)\\2A+2B&=4\quad&&(2)\\\frac{1}{3}A+B+2C&=4\quad&&(3)\end{alignat*}\)

Steps Calculations
  1. Rearrange equation (2).
 $$A=2-B\quad(4)$$
  1. Substitute equation (4) into equation (1).
 $$\begin{aligned}(2-B)+B+C&=4\quad(5)\\C&=2\end{aligned}$$
  1. Substitute equation (4) into equation (3).
 $$\begin{aligned}\frac{1}{3}(2-B)+B+2C&=4\quad(6)\\B&=-1\end{aligned}$$
  1. Substitute B and C into equation (1).
 $$\begin{aligned}A-1+2&=4\\A&=3\end{aligned}$$
Solution: $$(A,\;B,\;C:\;3,\;-1,\;2)\\\mathsf{or}\\3x-y+2z=4$$
Question 16

Each of the following equations represents a plane in 3-dimensional space.

Find the values for \(a\) and \(b\) so that geometrically the three planes meet in a single line.

$$\begin{aligned}ax + 3y + 2z &= b\\2x - y - 2z& = 16\\3x + 2y &= 10\end{aligned}$$

\(a = 1,\;b = - 6\)

Question 17

A system of equations is given as:

$$\begin{aligned}x - 2y + 5z& = 0\\2x + 4y + 9z &= 4\\-5x + ay + bz& = c\end{aligned}$$

  1. If this system of equations has no solution and the geometrical description is that two of the planes are parallel, find one possible set of values for \(a, b\) and \(c\) for this to occur.
  2. If the system of equations has multiple solutions, find one possible set of values for \(a, b\) and \(c\) for this to occur.
  1. If parallel to 1st plane, \(\frac{1}{-5}=\frac{-2}{a}=\frac{5}{b}\;\neq\;\frac{0}{c}\;\Rightarrow\;a = 10,\;b = -25,\;c \neq0\)
    If parallel to 2nd plane, \(\frac{2}{-5}=\frac{4}{a}=\frac{9}{b}\;\neq\;\frac{4}{c}\;\Rightarrow\;a = -10,\;b = -\frac{45}{2},\;c\neq-10\)
  2. There are many correct answers.
    Possible solution: \(a = 10,\;b = -25,\;c = 0\). Many other answers exist.
    All solutions are of the form: \(a = k,\;b=\frac{190+k}{-8},\;c=\frac{k-10}{2}\)
Question 18

The following is a system of equations:

$$\begin{aligned}2x + 5y - 3z& = 2\\3x + 9y - 2z &= 20\\-x + py + qz& = 0\end{aligned}$$

  1. The system of equations is inconsistent and the geometrical description is that two of the planes are parallel. State one possible set of values for the constants \(p\) and \(q\) that make this true.
  2. Assume the above set of equations has the unique solution, \(x = 1,y = 3,z = 5\). Find one set of values for the constants \(p\) and \(q\) that make this true.
  1. For equations (1) and (3) to be parallel: \(\frac{2}{-1} = \frac{5}{p} = \frac{-3}{q} , \quad p = \frac{-5}{2}, \quad q = \frac{3}{2}\)
    For equations (2) and (3) to be parallel: \(\frac{3}{-1} = \frac{9}{p} = \frac{-2}{q} , \quad p = -3, \quad q = \frac{2}{3}\)
    Note: Either pair of values, so 1 for \(p\), 1 for \(q\).
  2. Many possible solutions.
    All values of \(p\) and \(q\) must be of the form: \(p = k, \quad q = \frac{1 - 3k}{5}\). For example, \(p = 0,\;q = 0.2\) or \(p = -3,\;q = 2\).
Question 19

The following system of equations is dependent.

$$\begin{alignat*}{2}-x + 2y + 3z &= -2\quad&(1)\\2x + y + 2z &= -3\quad&(2)\\-11x + 2y + z &= 6\quad&(3)\end{alignat*}$$

  1. Find the values of \(a\) and \(b\) in the equation:
    $$\mathsf{Equation}\;(3) = [a\times\mathsf{Equation}\;(1)] + [b \times\mathsf{Equation}\;(2)]$$
  2. Find a solution for this system of equations.
  1. \(a = 3,\;b = -4\)
  2. For example, \((0,\;5, \;− 4)\) or any one of \((k,\;8k + 5,\;-5k-4)\).
Question 20

A garage owner hires three people. Their combined hourly wage is $46. The difference between the highest wage and the lowest wage is $3 per hour. The highest and lowest paid workers work for 2 hours and the other works for 3 hours. The total wage bill is $107.

  1. Write 3 equations with the information provided and solve the system of equations.
  2. What are the hourly rates for each of the workers?
  1. Let the pay per hour for each person be \(a,\; b\) and \(c\):
    \(\begin{aligned} a + b + c &= 46 \\ a - b &= 3 \\ 2a + 2b + 3c &= 107 \\ \end{aligned}\)
  2. Solution: \(a = \$17\) per hour; \(b = \$14\) per hour; and \(c = \$15\) per hour.

The following are the key terms for this topic. You should have a good understanding of what each term means and how to use it correctly. Write a definition for each term in your own words in your notes.

  • Coefficient
  • Coincident
  • Constant
  • Dependent
  • Elimination
  • Equate
  • Equation
  • Geometric
  • Inconsistent
  • Intersect
  • Multiple
  • Parallel
  • Plane
  • Product
  • Solution
  • Solve
  • Substitution
  • Term
  • Unique
  • Undefined
  • Unknown
  • Variable

Snyder, MH 2023, Sciencing, 10 Ways Simultaneous Equations Can Be Used in Everyday Life, Leaf Group Media, viewed 11 August 2023, <https://sciencing.com/everyday-examples-situations-apply-quadratic-equations-10200.html>.

Module Linking
UOADEMO2
Main Topic Image
Air traffic control radar image showing the flight paths of several planes.
Is Study Guide?
Off
Is Assessment Consultation?
Off